Sensor for locating sound sources: Difference between revisions
| (70 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
===Acoustic source location identification=== | ===Acoustic source location identification=== | ||
====1-Dimensional==== | ====1-Dimensional==== | ||
[[File:1D1.jpg|500px]] | [[File:1D1.jpg|thumb|none|500px|Fig.1 1D]] | ||
<math>C</math> : Speed of sound in air (~340m/s) <br> | <math>C</math> : Speed of sound in air (~340m/s) <br> | ||
According to the mathematical relationship <br> | According to the mathematical relationship <br> | ||
| Line 19: | Line 19: | ||
====2-Dimensional==== | ====2-Dimensional==== | ||
[[File:2D.png|500px]] | [[File:2D.png|thumb|none|500px|Fig.2 2D]] | ||
We can tell that the mathematical relationship are <br> | We can tell that the mathematical relationship are <br> | ||
<math>r = \frac{L}{\sqrt{3}}</math>, <br> | <math>r = \frac{L}{\sqrt{3}}</math>, <br> | ||
| Line 45: | Line 45: | ||
====3-Dimensional==== | ====3-Dimensional==== | ||
[[File: | [[File:3D1.jpg|thumb|none|500px|Fig.3 3D]] | ||
We can tell that the mathematical relationship are <br> | We can tell that the mathematical relationship are <br> | ||
<math>d_2^2 = x^2 + y^2 + z^2</math>, <br> | <math>d_2^2 = x^2 + y^2 + z^2</math>, <br> | ||
| Line 51: | Line 51: | ||
<math>\Rightarrow d_1^2 - d_2^2 = d^2 - 2xd</math>, <br><br> | <math>\Rightarrow d_1^2 - d_2^2 = d^2 - 2xd</math>, <br><br> | ||
<math>\sqrt{x^2 + y^2 + z^2} = d_2 = \frac{2d_1^2 - 2xd_1}{2(d_2 - d_1)}</math>. <br> | <math>\sqrt{x^2 + y^2 + z^2} = d_2 = \frac{2d_1^2 - 2xd_1}{2(d_2 - d_1)}</math>. <br> | ||
<math>= \frac{1}{2(d_2 - d_1)} (d_1^2 + d_2^2 - 2xd_1 - d_1^2 + d_2^2)</math> <br> | |||
<math>= \frac{1}{2(d_2 - d_1)} [(d_2 - d_1)^2 - d_1^2 + d_2^2]</math> <br> | |||
<math>= \frac{1}{2C \cdot \Delta t_{21}} [(C \cdot \Delta t_{21})^2 + 2xd_1 - d_1^2]</math>. <br><br> | |||
In the same way, we can get <br> | In the same way, we can get <br> | ||
<math>= \frac{1}{ | |||
<math>= \frac{1}{ | <math>\sqrt{x^2 + y^2 + z^2} = d_2 = \frac{1}{2C \cdot \Delta t_{23}} \left[(C \cdot \Delta t_{23})^2 + 2dy - d^2\right]</math>, <br> | ||
<math>= \frac{1}{2C \cdot \Delta t_{ | <math>\sqrt{(x - D)^2 + y^2 + z^2} = d_4 = \frac{1}{2C \cdot \Delta t_{45}} \left[(C \cdot \Delta t_{45})^2 - 2dx(x - D)\right]</math>, <br> | ||
<math>\sqrt{(x - D)^2 + y^2 + z^2} = d_4 = \frac{1}{2C \cdot \Delta t_{46}} \left[(C \cdot \Delta t_{46})^2 + 2Dx + D^2 - 2dy - d^2\right]</math>. <br> | |||
So we can get the relationship between x and y,<br> | So we can get the relationship between x and y,<br> | ||
| Line 93: | Line 98: | ||
Now <math>X(\omega)</math> is the Fourier transform of <math>x(t)</math>,<math>Y(\omega)</math> is the conjugate Fourier transform of <math>y(t)</math>. Some of <math>\omega</math>, the integral might correspond to the maximum value of <math>\phi_{xy}(t)</math>. Therefore, correlations can be quickly calculated by Fourier transforms and conjugate Fourier transforms. | Now <math>X(\omega)</math> is the Fourier transform of <math>x(t)</math>,<math>Y(\omega)</math> is the conjugate Fourier transform of <math>y(t)</math>. Some of <math>\omega</math>, the integral might correspond to the maximum value of <math>\phi_{xy}(t)</math>. Therefore, correlations can be quickly calculated by Fourier transforms and conjugate Fourier transforms. | ||
== | ==Experimental Setup== | ||
1. LeCroy - WaveSurfer - 64Xs - 600MHz Oscilloscope <br> | 1. LeCroy - WaveSurfer - 64Xs - 600MHz Oscilloscope <br> | ||
[[File:Oscilloscope.jpg|thumb|none|300px|LeCroy - WaveSurfer - 64Xs - 600MHz Oscilloscope]] | [[File:Oscilloscope.jpg|thumb|none|300px|Fig.4 LeCroy - WaveSurfer - 64Xs - 600MHz Oscilloscope]] | ||
2. 3 integrated microphones (Adafruit AGC Electret Microphone Amplifier - MAX9814) <br> | 2. 3 integrated microphones (Adafruit AGC Electret Microphone Amplifier - MAX9814) <br> | ||
[[File:micro1.png|thumb|none|300px|Adafruit AGC Electret Microphone Amplifier - MAX9814]] | [[File:micro1.png|thumb|none|300px|Fig.5 Adafruit AGC Electret Microphone Amplifier - MAX9814]] | ||
3. Breadboard<br> | 3. Breadboard<br> | ||
4. Cables<br> | 4. Cables<br> | ||
5. 4.5V power supply<br> | 5. Tape measure<br> | ||
[[File:completesetup.jpg|thumb|none|300px| | 6. 4.5V power supply<br> | ||
[[File:completesetup.jpg|thumb|none|300px|Fig.6 Completely built device]] | |||
==Measurements== | ==Measurements== | ||
=== | ===1-Dimensional=== | ||
1. One microphone was placed at 0cm as a reference and trigger, and the other microphone was placed 200cm away from it in a straight line. Both microphones were connected to an oscilloscope to obtain the waveform of the sound. (In the test experiments, we also set the straight line distance between the two microphones to 380cm, 100cm, etc.)<br> | |||
{| class="wikitable" style="margin-left:auto; margin-right:auto;" | |||
|- | |||
| [[File:wideview.png|thumb|320px|Fig.7(a) Microphone and Oscilloscope Setup]] | |||
| [[File:close-upview.jpg|200px|thumb|Fig.7(b) close-up view]] | |||
|} | |||
2. At 0, 50, 100, 150, and 200 cm points along the line between the two microphones, different sounds were produced, including clapping, and vocal sounds like "a", "hello", and "yes". The waveforms captured by the microphones were recorded on the oscilloscope.<br> | |||
[[File:hello150cm.jpg|thumb|center|350px|Fig.8 'Hello' at 150.00cm]] | |||
=== | 3.In the extended experiment, we tried the same experiment as step 2 on the outside of the two microphones, i.e. -50, 250 cm.<br> | ||
4. MATLAB was used to analyze the recorded data. This involved calculating the time differences of arrival (TDOAs) of the sounds at the two microphones, from which the precise locations of the sounds were determined.<br> | |||
===2-Dimensional=== | |||
1. Three microphones are placed on the three vertices of an equilateral triangle with a side length of 2m.<br> | |||
2. At the same time, we marked the position of the center of gravity of the equilateral triangle.<br> | |||
{| class="wikitable" style="margin-left:auto; margin-right:auto;" | |||
|- | |||
| [[File:wideview_2D.png|thumb|320px|Fig.9(a) Microphone and Oscilloscope Setup]] | |||
| [[File:core.png|320px|thumb|Fig.9(b) The core of equilateral triangle]] | |||
|} | |||
3. At any position, speech commands "yes" are produced. The waveforms captured by the microphones were recorded on the oscilloscope.<br> | |||
4. MATLAB was used to analyze the recorded data. This involves calculating the difference in time of arrival (TDOAs) of the sound at any two microphones, from which the precise location of the sound is determined.<br> | |||
==Data Processing== | ==Data Processing== | ||
| Line 130: | Line 155: | ||
'''Visualization''' | '''Visualization''' | ||
* Amplitude offsets for each microphone were plotted in a shared graph with distinct colors (red for Microphone 1 and blue for Microphone 2) to ensure clear differentiation. | * Amplitude offsets for each microphone were plotted in a shared graph with distinct colors (red for Microphone 1 and blue for Microphone 2) to ensure clear differentiation. | ||
{| class="wikitable" style="margin-left:auto; margin-right:auto;" | |||
{| class="wikitable" | |- | ||
| [[File:clapwave.png|280px|thumb|Fig.10(a) Sound source type: Clap]] | |||
| [[File:hellowave.png|280px|thumb|Fig.10(b) Sound source type: 'Hello']] | |||
|- | |- | ||
| [[File: | | [[File:yeswave.png|280px|thumb|Fig.10(c) Sound source type: 'Yes']] | ||
| [[File:awave.png|280px|thumb|Fig.10(d) Sound source type: 'A']] | |||
| [[File:awave.png|280px|thumb| | |||
|} | |} | ||
| Line 213: | Line 238: | ||
% Output normalized calculation results | % Output normalized calculation results | ||
disp(['Normalized Time Difference: ', num2str(time_diff_norm), ' seconds']); | disp(['Normalized Time Difference: ', num2str(time_diff_norm), ' seconds']); | ||
==== 2-Dimensional ==== | |||
ch_0 = load('C1Trace00001.dat'); | |||
ch_1 = load('C2Trace00041.dat');% trigger, reference | |||
ch_2 = load('C4Trace00035.dat'); % Assuming filename and format | |||
L = 2; % dist btw 2 microphones | |||
c = 340; % speed of sound in ms^-1 | |||
time = ch_0(:, 1); | |||
dtime = ch_0(2, 1)- ch_0(1, 1); | |||
ch_0_ampl = ch_0(:, 2); | |||
ch_1_ampl = ch_1(:, 2); | |||
ch_0_ampl_mean = mean(ch_0_ampl); | |||
ch_1_ampl_mean = mean(ch_1_ampl); | |||
ch_0_ampl_offset = ch_0_ampl - ch_0_ampl_mean; | |||
ch_1_ampl_offset = ch_1_ampl - ch_1_ampl_mean; | |||
ch_2_ampl = ch_2(:, 2); | |||
ch_2_ampl_mean = mean(ch_2_ampl); | |||
ch_2_ampl_offset = ch_2_ampl - ch_2_ampl_mean; | |||
% Adjust time vector to start from 0 | |||
time_adj = time - time(1); % Subtract the first time value from all elements | |||
[c12, lag12] = xcorr(ch_0_ampl_offset, ch_1_ampl_offset); | |||
[c13, lag13] = xcorr(ch_0_ampl_offset, ch_2_ampl_offset); | |||
[c23, lag23] = xcorr(ch_1_ampl_offset, ch_2_ampl_offset); | |||
[val12, index12] = max(c12); | |||
[val13, index13] = max(c13); | |||
[val23, index23] = max(c23); | |||
Delta_t12 = dtime * lag12(index12); | |||
Delta_t13 = dtime * lag13(index13); | |||
Delta_t23 = dtime * lag23(index23); | |||
% Define the symbols | |||
syms R phi | |||
r = L / sqrt(3); % Distance from each microphone to the centroid of the triangle | |||
eq1 = sqrt(R^2 + r^2 - 2*R*r*cos(phi + 2*pi/3)) - sqrt(R^2 + r^2 - 2*R*r*cos(2*pi/3 - phi)) == c * Delta_t12; | |||
eq2 = sqrt(R^2 + r^2 - 2*R*r*cos(phi)) - sqrt(R^2 + r^2 - 2*R*r*cos(phi + 2*pi/3)) == c * Delta_t13; | |||
eq3 = sqrt(R^2 + r^2 - 2*R*r*cos(2*pi/3 - phi)) - sqrt(R^2 + r^2 - 2*R*r*cos(phi)) == c * Delta_t23; | |||
% Solve the system of equations | |||
[solution_R, solution_phi] = solve([eq1, eq2, eq3], [R, phi], 'Real', true); | |||
%[solution_R, solution_phi] = solve([eq2, eq3], [R, phi], 'Real', true); | |||
% Calculate numerical solutions | |||
num_solution_R = vpa(solution_R); | |||
num_solution_phi = vpa(solution_phi); | |||
% Display the solutions | |||
disp('Solution for R:'); | |||
disp(num_solution_R); | |||
disp('Solution for phi:'); | |||
disp(num_solution_phi); | |||
==Results== | ==Results== | ||
===1-Dimensional=== | ===1-Dimensional=== | ||
====Relationship between time lags and theoretical locations==== | |||
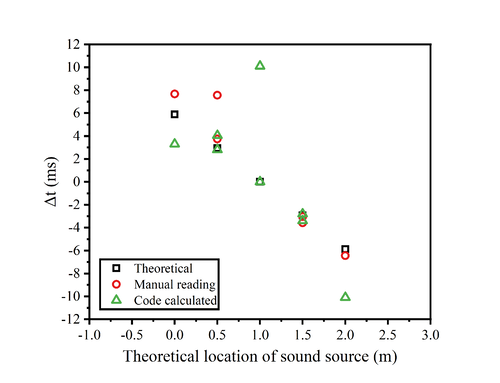
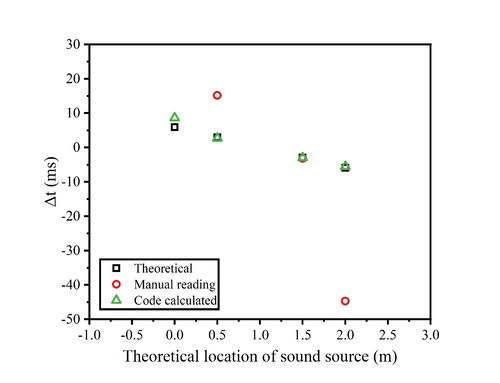
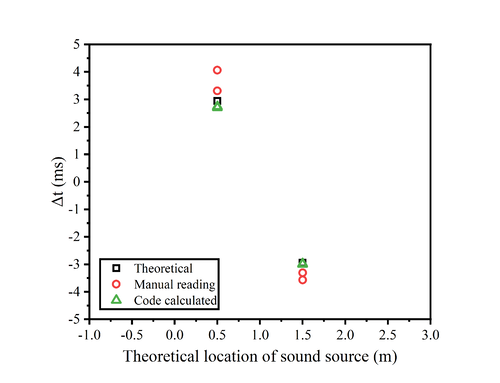
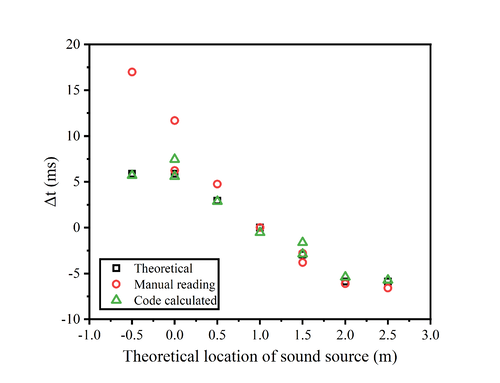
The inherent subjectivity of human observation often poses challenges in accurately determining the relative positions of sound waves, potentially leading to significant measurement errors. Consequently, reliance on the oscilloscope's direct reading of time differences (Δt) may yield results of questionable reliability.<br> | |||
The figure presented below delineates the relationship between the time lags and theoretical locations for four distinct types of sound sources. On the graph, three varieties of data markers are employed: squares denote the theoretical data points; circles correspond to manual readings; and triangles are indicative of the results computed by the code.<br> | |||
{| class="wikitable" style="margin-left:auto; margin-right:auto;" | |||
|- | |||
| [[File:clapdeltat.png|500px|thumb|Fig.11(a) Time lags vs theoretical location (Sound source type: Clap)]] | |||
| [[File:hellodeltat.png|500px|thumb|Fig.11(b) Time lags vs theoretical location (Sound source type: 'Hello')]] | |||
|- | |||
| [[File:adeltat.png|500px|thumb|Fig.11(c) Time lags vs theoretical location (Sound source type: 'A')]] | |||
| [[File:yesdeltat.png|500px|thumb|Fig.11(d) Time lags vs theoretical location (Sound source type: 'Yes')]] | |||
|} | |||
An intuitive assessment of the figure clarifies that the code-derived computational results exhibit markedly greater accuracy than those obtained through manual oscilloscope measurements. Utilizing the measured Δt, the position of the sound source can be calculated, which will be methodically analyzed in the subsequent section.<br><br> | |||
==== | ====Relationship between calculated locations and theoretical locations==== | ||
=====Clap===== | =====Clap===== | ||
====='Hello'===== | In our experiments, we first chose a single clap as the sound source. Multiple measurements were taken by clapping at locations between the two microphones, i.e., at 0, 50, 100, 150, and 200 cm, and the results are shown below.<br> | ||
== | {| class="wikitable" style="margin-left:auto; margin-right:auto;" | ||
|- | |||
| [[File:clap.png|thumb|500px|Fig.12(a) Sound source type: Clap]] | |||
== | | [[File:erro_clap.png|500px|thumb|Fig.12(b) Relative error (Sound source type: Clap)]] | ||
|} | |||
The figure shows the relationship between the theoretical position of the sound source and the calculated position. Since the horizontal coordinate is the theoretical position of the sound source, the vertical coordinate corresponding to the red straight line is the theoretical position of the sound source, so it is used as the reference line. The black square is the calculated sound source position.<br> | |||
=== | Comparing the positions of the black square and the red line, it is found that the measurement error is larger at 0cm and 200cm (i.e., the positions of the two microphones), while the error is smaller at the position between the two microphones, and the closer to the midpoint of the two microphones, the closer to the theoretical position of the sound source is the calculated position of the sound source. One of the points fell farther below the reference line when the theoretical position was 1.0 m. It is speculated that this may be due to an operational error during the measurement process.<br> | ||
In order to better compare the error between the theoretical position and the calculated position, we calculated its relative error. From the figure, we can find that the relative errors of the measurements basically fall below 0.5% except for the one measurement that was operated incorrectly. The closer the sound source position is to the midpoint of the two microphones, the smaller the relative error is. When the sound source position is 1.0m, the relative error is only about 0.0005%, which almost indicates that the calculated position is the same as the theoretical position.<br><br> | |||
=====Speech Commands: 'Hello', 'A', 'Yes'===== | |||
Due to the large error, we replaced the sound source with speech commands: 'Hello', 'A', 'Yes'. The experiment was repeated and the results obtained are shown in Fig.<br> | |||
{| class="wikitable" style="margin-left:auto; margin-right:auto;" | |||
|- | |||
| [[File:hello.png|500px|thumb|Fig.13(a) Sound source type: 'Hello']] | |||
| [[File:erro_hello.png|500px|thumb|Fig.13(b) Relative error (Sound source type: 'Hello')]] | |||
|- | |||
| [[File:A.png|500px|thumb|Fig.13(c) Sound source type: 'A']] | |||
| [[File:erro_a.png|500px|thumb|Fig.13(d) Relative error (Sound source type: 'A')]] | |||
|} | |||
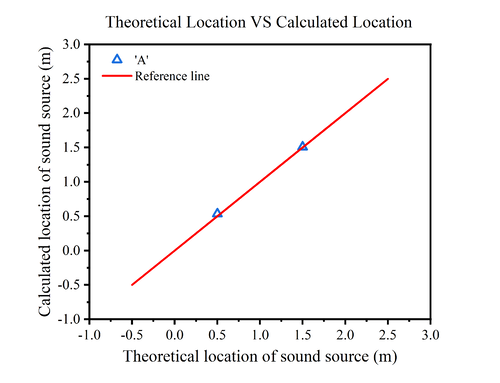
In Fig.13(a), we replace the sound source with the speech command: 'hello', and we can find that the calculated position at 0cm has a large error with the theoretical position, while the remaining points are almost on the reference line. In Fig.13(c), the sound source is the speech command: 'A', four experiments were conducted at distances of 0.5m and 1.5m. It shows that the four calculated results closely align, and the theoretical positions are almost identical to the calculated positions.<br> | |||
It can be noticed that when we change the sound source from clapping to speech command, the error decreases. However, there is still a higher probability of error when the sound source is at both ends, while in the middle of the two microphones, our measurements and code calculations are able to call a more accurate location of the sound source.<br> | |||
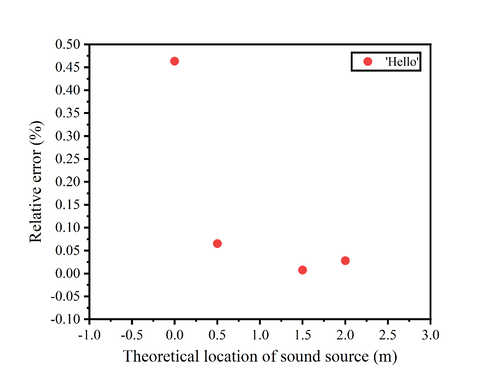
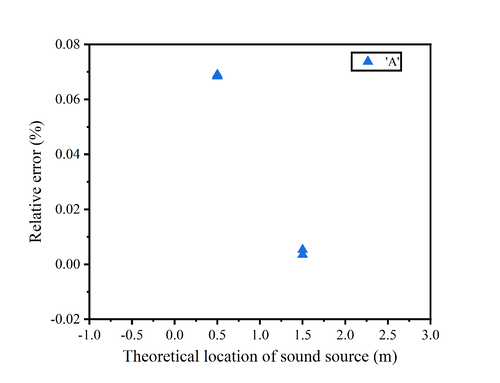
The image of the relative error of 'hello' shows that only the measurement at 0cm has a large relative error of about 0.47%, while the rest of the measurements have a relative error of less than 0.1%. In contrast to the relative error produced by clapping, there is a significant reduction using the speech command. The image of the relative error of 'A' shows that the relative error of both measurements is 0.07% when the theoretical position is at 0.5m. When the theoretical position is at 1.5m, the relative error of both measurements is almost close to zero.<br><br> | |||
We also conducted several experiments when the sound source was 'yes', and in addition to measuring between the two microphones, we set the source at -50cm and 150cm for measurements.<br> | |||
{| class="wikitable" style="margin-left:auto; margin-right:auto;" | |||
|- | |||
| [[File:yes.png|thumb|500px|Fig.14(a) Sound source type: 'Yes']] | |||
| [[File:erro_yes.png|500px|thumb|Fig.14(b) Relative error (Sound source type: 'Yes')]] | |||
|} | |||
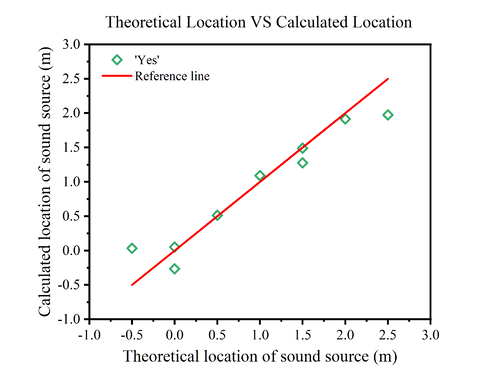
One measurement at 0cm and another at 150cm produced errors, so we conducted a second experiment at the same location and obtained better results at both points. This shows that the determination of the sound source position may be subject to errors due to some accidental factors. Since we used a mobile phone to play a speech command, it is possible that the orientation of the mobile phone may have an effect on the results.<br> | |||
Also, we notice that when we set the sound at -50, 250cm, the calculated positions are almost at the theoretical positions of 0cm and 200cm. This is in accordance with the theory that, assuming the sound is at -50cm, the difference in time for the sound to reach the two microphones is exactly the time difference caused by the distance between the two microphones. Therefore, it is clear from the measurements that the device is not able to obtain the position of the sound source on the outside of the two microphones.<br> | |||
The relative error image of 'yes' reveals that one measurement at point 0 produces a large error of about 0.3%, while the rest of the measurements between 0-2.0m have a relative error of almost 0.15% or less. As we know from the previous description, it is not possible to determine the location of the sound source at the outside of the two microphones, so the relative error at the two points is larger, especially at -0.5m, where the relative error is about 1.1%.<br><br> | |||
=====Aggregate Sound Source Positioning===== | |||
We have summarised all the measurements on a single graph in order to check the performance of the sensor more clearly.<br> | |||
{| class="wikitable" style="margin-left:auto; margin-right:auto;" | |||
|- | |||
| [[File:all.png|thumb|none|500px|Fig.15(a) Relationship between theoretical and calculated positions]] | |||
| [[File:erro.png|500px|thumb|Fig.15(b) Relative error]] | |||
|} | |||
The figure shows the position measurements of the sensor for different sound sources at different locations. It can be noticed that the sensor performance is poorer and the error is larger when the sound is at the ends, and the closer the sound is to the midpoint of the two microphones, the smaller the measurement error is.<br> | |||
It is surmised that this may be because the closer the sound is to a particular microphone, the more sensitively variations can be reacted to this microphone. And when the sound is close to the middle, the resulting changes will be captured to the same extent by both microphones.<br> | |||
Clapping as a sound source may have a greater error than voice commands. This may be due to the fact that clapping sounds are more brief and sharp, which are less coherent and of short duration, making it difficult to extract precise temporal information from clapping sounds. Moreover, hand-clapping sounds contain a wide frequency range, including many high-frequency components, which may be subject to more attenuation and scattering during propagation, thus affecting measurement accuracy. On the contrary, voice commands have a long duration, a more regular and consistent acoustic pattern, a more concentrated frequency range, and a more stable acoustic signal.<br> | |||
In addition, there may be chance factors that affect the accuracy of the measurement, and multiple measurements may be required if accuracy is desired.<br> | |||
The relative error shows that excluding operational errors and measurements at -0.5m and 2.5m, we can keep the relative error below 0.5%, and even below 0.1% when the source is close to the midpoint of the two microphones. This shows that our sensor can accurately measure the position of the sound source in one dimension.<br> | |||
==Error Analysis and Discussions== | ==Error Analysis and Discussions== | ||
| Line 234: | Line 364: | ||
=== Human factors === | === Human factors === | ||
* '''Optimal Parameter Settings''': | * '''Optimal Parameter Settings''': | ||
** Finding the most accurate setting for measurement parameters is crucial. Incorrect settings can lead to insufficient precision, significantly impacting the calculated results and the actual sound source location. | ** Finding the most accurate setting for measurement parameters is crucial. Incorrect settings can lead to insufficient precision, significantly impacting the calculated results and the actual sound source location. | ||
| Line 265: | Line 391: | ||
It is imperative to meticulously consider and, where possible, quantify each potential source of error. By doing so, the interpretation of data can be significantly enhanced, improving the reliability of the sound source localization methodology. | It is imperative to meticulously consider and, where possible, quantify each potential source of error. By doing so, the interpretation of data can be significantly enhanced, improving the reliability of the sound source localization methodology. | ||
=== | === Possibility of improvement === | ||
==== | |||
==== | ==== Improvement of experimental equipment ==== | ||
==== | |||
In order to improve the accuracy and repeatability of sound detection when the equipment is more fragmented and lacks a complete automation system, the following is an expanded description for each aspect: | |||
* '''Fixed microphone position''': Design and implement a stand or shelf to fix the microphone in a suitable position to ensure that the distance between them is always consistent. | |||
* '''Noise control''': In order to reduce the noise that may be introduced, a number of measures can be taken. Place the experimental equipment in a relatively quiet environment, away from sources that may produce noise. Or use sound insulation materials such as foam or sponge board to isolate the sound source, and arrange sound insulation materials around the microphone to absorb ambient noise. | |||
* '''Replace more advanced experimental equipment ''': Consider updating the microphone sensor and oscilloscope in the equipment to a more advanced model. Choose a microphone sensor with higher sensitivity and a wider frequency response range to ensure that you can capture a more accurate and rich sound signal. Through the use of advanced equipment, the quality and accuracy of sound data can be significantly improved, thus enhancing the credibility and repeatability of experimental results. | |||
====Algorithm improvement==== | |||
* '''Code Efficiency''': Preallocate memory for large matrices as we know their size beforehand to improve performance. For loops that can be vectorized, do so to utilize MATLAB’s optimized matrix operations. | |||
* '''Code Modularity''': Consider breaking it into functions or scripts for better reuse and modularity. | |||
====Others==== | |||
In order to make the device more multi-functional and intelligent, and more practical prospects, the following functions can be considered: | |||
* '''Specific voice recognition''': Integrated speech recognition software or algorithms allow the device to recognize specific voice patterns or frequencies. This capability can be used by training the model to recognize specific sounds, such as a specific command, the sound of a specific object, or noises common in the environment. By identifying specific sounds, such as those coming from different directions or specific locations, it is possible to infer the direction or location from which the sound may have come. For example, if the device is able to recognize that a particular sound pattern is coming from the left and another particular sound pattern is coming from the right, their relative positions can be inferred. Recognizing a particular sound, the device can take preset actions, such as triggering an alarm, recording data, or executing specific control commands. Such a function can improve the intelligence level of the device and make it more suitable for various application scenarios. | |||
* '''Sound analysis function''': The device can have sound analysis function for in-depth analysis of sound spectrum, intensity and other information. Through a more detailed analysis of the sound, the source, type and characteristics of the sound can be identified. The sound characteristics provided by the sound analysis function also help further identify the source and location of the sound. Therefore, the recognition of specific sounds and the analysis of sounds can provide important auxiliary information for sound location, thus enhancing the positioning accuracy and reliability of the device. | |||
==[[Logs]]== | ==[[Logs]]== | ||
Build a link to record experiment log. | Build a link to record experiment log. Please click me!!! | ||
==References== | ==References== | ||
* 2D theory: https://patentimages.storage.googleapis.com/a9/99/44/a66234cb68ab63/CN103995252B.pdf<br> | |||
* 3D theory: https://patentimages.storage.googleapis.com/7d/26/47/a6bce6afc723c6/CN103064061B.pdf<br> | |||
* Microphone datasheet: https://cdn-learn.adafruit.com/downloads/pdf/adafruit-agc-electret-microphone-amplifier-max9814.pdf<br> | |||
* Oscilloscope datasheet: https://www.testequipmenthq.com/datasheets/LECROY-WAVESURFER%2064XS-Datasheet.pdf<br> | |||
* TDOA theory: https://iot-book.github.io/13_%E6%97%A0%E7%BA%BF%E5%AE%9A%E4%BD%8D/S2_TDOA%E5%AE%9A%E4%BD%8D%E7%AE%97%E6%B3%95/<br> | |||
==[[Sensor that recognizes specific sounds and steers toward the source]]== | ==[[Sensor that recognizes specific sounds and steers toward the source]]== | ||
This is the name and link of the previous page. We adjusted the final project name displayed on the main page based on the final results and conditions. | This is the name and link of the previous page. We adjusted the final project name displayed on the main page based on the final results and conditions. | ||
Latest revision as of 00:02, 28 April 2024
Team Members
Wang Liyue, Li Jiaqi, Su Qiqi, Wang Tongxu
Introduction
The ability to accurately locate sound sources has extensive applications ranging from audio surveillance to enhancement in hearing aids. This project aims to develop a sensor capable of pinpointing sound origins using a microphone array system.
Our approach involves the construction of an array consisting of multiple microphones strategically positioned to capture sound waves from various directions. The core of our sensor's computational framework relies on the cross-correlation function. This algorithm determines the time differences of arrival (TDOAs) of sound waves at different microphones. By computing these TDOAs, we can effectively estimate the direction and distance of the sound source relative to the array, enabling precise localization. Upon assembling the experimental setup, the performance of the sensor was initially validated in a one-dimensional context. Subsequently, the theoretical groundwork and algorithmic coding were extended to more complex two-dimensional and three-dimensional scenarios, enhancing the sensor's applicability across different environments.
Future enhancements will involve expanding the microphone array configuration. In two-dimensional setups, a minimum of three microphones is essential for accurate localization, while three-dimensional configurations require an even greater number. Beyond merely identifying sound locations, we aim to integrate machine learning to distinguish specific sounds and enable mechanical responses to auditory stimuli. By exemplifying the potential of this technology, we could, for instance, discern and locate different individuals by their voice signatures. Integrating this capability with devices like cameras could achieve a sophisticated level of 'voiceprint monitoring/detection,' showcasing the broad utility of our approach.
Theory
Acoustic source location identification
1-Dimensional
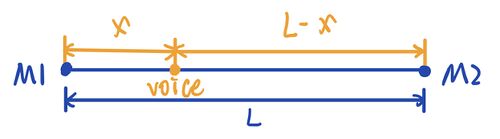
: Speed of sound in air (~340m/s)
According to the mathematical relationship
,
we can know the position of voice. However, this has a drawback, when the sound source is not between the microphone M1M2 we can not tell its position.
2-Dimensional
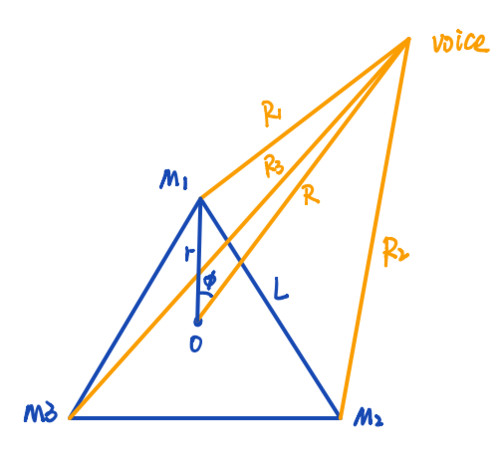
We can tell that the mathematical relationship are
,
,
,
.
And the distance difference:
,
,
.
So we can get
,
,
.
If the is greater than , we will take as the angle of the , (i.e., the source is in the left plane divided by the line between the centre of gravity and M1) so that the angle of the stays between -.
In this case:
,
,
.
The distance difference:
,
,
.
Since we can measure and calculate the difference in distance between M2 and M3 (i.e. ), the first and second mathematical relationships are solved in terms of joint equations for and , respectively.
Then we can get , and know the position of voice.
3-Dimensional
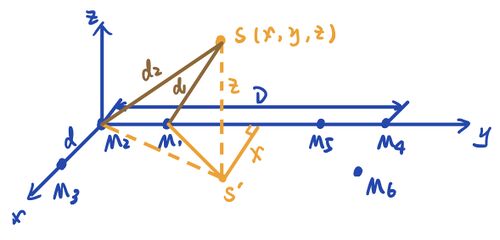
We can tell that the mathematical relationship are
,
,
,
.
.
In the same way, we can get
,
,
.
So we can get the relationship between x and y,
,
which
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_1 = \frac{\Delta t_{23}}{\Delta t_{21}}}
,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_1 = \frac{(C^2 \cdot \Delta t_{21} \cdot \Delta t_{23} + d^2)(\Delta t_{21} - \Delta t_{23})}{2d \cdot \Delta t_{21}}}
.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = a_2x + b_2}
,
which
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_2 = -\frac{\Delta t_{46}}{\Delta t_{45}}}
,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_2 = \frac{\left[(C^2 \cdot \Delta t_{45} \cdot \Delta t_{46} + d^2)(\Delta t_{45} - \Delta t_{46}) + 2dD\Delta t_{45}\right]}{2d \cdot \Delta t_{45}}}
.
Using these two formulas
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = a_1x + b_1}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = a_2x + b_2}
,
we can get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \hat{x} = \frac{b_2 - b_1}{a_1 - a_2}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{y} = \frac{a_1b_2 - a_2b_1}{a_1 - a_2}}
.
By inserting (x,y) into the distance difference formula, we can find the z value. Get the voice position S (x,y,z).
Cross-Correlation Function
Correlation function is a concept in signal analysis, representing the degree of correlation between two time series, that is, describing the degree of correlation between the values of signal x(t) and y(t) at any two different times t1 and t2. When describing the correlation between two different signals, the two signals can be random signals or they can be deterministic signals.
The correlation function can be used to calculate the arrival time difference of two sound signals, assuming that the signal received by microphone M1 is x(t), the signal received by microphone M2 is y(t)=Ax(t−t0), and the arrival time difference between sound waves arriving M1 and M2 is t0. Then the cross-correlation function of x(t) and y(t) is defined as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{xy}(t) = \int_{-\infty}^{+\infty} x(\tau)y(t + \tau) d\tau = x(t) * y(-t)}
.
Substituting the y(t) expression yields:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{xy}(t) = \int_{-\infty}^{+\infty} x(\tau)x(t + \tau - t_0) d\tau}
,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{when } t = t_0 \text{, we can get the maximun of } \phi_{xy}(t) = \int_{-\infty}^{+\infty} x(\tau)^2 d\tau.}
According to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x(t) * y(-t) = X(\omega)Y^*(\omega)}
,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{xy}(t) = \int_0^{\pi} X(\omega)Y^*(\omega) e^{-j\omega t} d\omega}
Now is the Fourier transform of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x(t)} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y(\omega)} is the conjugate Fourier transform of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(t)} . Some of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} , the integral might correspond to the maximum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{xy}(t)} . Therefore, correlations can be quickly calculated by Fourier transforms and conjugate Fourier transforms.
Experimental Setup
1. LeCroy - WaveSurfer - 64Xs - 600MHz Oscilloscope

2. 3 integrated microphones (Adafruit AGC Electret Microphone Amplifier - MAX9814)

3. Breadboard
4. Cables
5. Tape measure
6. 4.5V power supply

Measurements
1-Dimensional
1. One microphone was placed at 0cm as a reference and trigger, and the other microphone was placed 200cm away from it in a straight line. Both microphones were connected to an oscilloscope to obtain the waveform of the sound. (In the test experiments, we also set the straight line distance between the two microphones to 380cm, 100cm, etc.)
 |
 |
2. At 0, 50, 100, 150, and 200 cm points along the line between the two microphones, different sounds were produced, including clapping, and vocal sounds like "a", "hello", and "yes". The waveforms captured by the microphones were recorded on the oscilloscope.
3.In the extended experiment, we tried the same experiment as step 2 on the outside of the two microphones, i.e. -50, 250 cm.
4. MATLAB was used to analyze the recorded data. This involved calculating the time differences of arrival (TDOAs) of the sounds at the two microphones, from which the precise locations of the sounds were determined.
2-Dimensional
1. Three microphones are placed on the three vertices of an equilateral triangle with a side length of 2m.
2. At the same time, we marked the position of the center of gravity of the equilateral triangle.
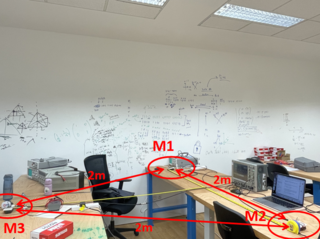 |
 |
3. At any position, speech commands "yes" are produced. The waveforms captured by the microphones were recorded on the oscilloscope.
4. MATLAB was used to analyze the recorded data. This involves calculating the difference in time of arrival (TDOAs) of the sound at any two microphones, from which the precise location of the sound is determined.
Data Processing
1-Dimensional
Data Collection
- Raw audio data were collected with two microphones, each recording saved as a '.dat' file.
- MATLAB was utilized for data importation and preliminary analysis.
Data Analysis Steps
- Data Loading: Each microphone's data was loaded into MATLAB.
- Distance Setting: A fixed distance of 'L' meters was maintained between both microphones.
- Time and Amplitude Extraction: Time-stamped amplitude data were extracted from the audio files.
- Amplitude Normalization: DC offset was mitigated by subtracting the mean amplitude from each signal.
- Time Vector Adjustment: The time vector was recalibrated to start at zero, synchronizing the datasets.
Visualization
- Amplitude offsets for each microphone were plotted in a shared graph with distinct colors (red for Microphone 1 and blue for Microphone 2) to ensure clear differentiation.
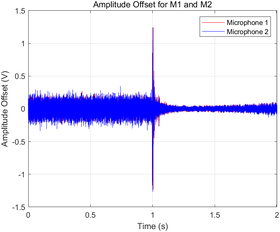 |
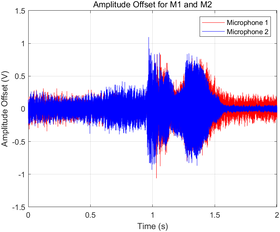 |
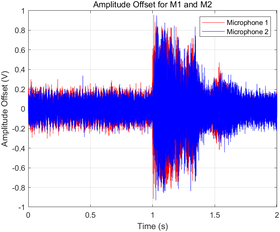 |
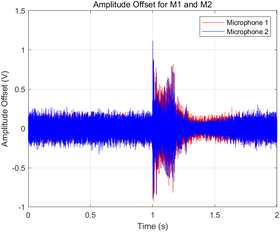 |
Cross-Correlation Analysis
- Temporal delays between signals were quantified through cross-correlation, pinpointing the sound's origination point relative to the microphones.
Sound Source Localization
- Employing the speed of sound (340 m/s), the source's location was computed based on the calculated time lag between the two signals.
Documentation and Output
- MATLAB commands were scripted to automate the processing steps, including normalization and cross-correlation plotting.
- The calculated time differences, delta distances, and source positions were output to the MATLAB console.
MATLAB code
1-Dimensional
ch_0 = load('C1Trace00000.dat');
ch_1 = load('C2Trace00000.dat'); % trigger, reference
L = 2; % dist btw 2 microphones
time = ch_0(:, 1);
dtime = ch_0(2, 1)- ch_0(1, 1);
ch_0_ampl = ch_0(:, 2);
ch_1_ampl = ch_1(:, 2);
ch_0_ampl_mean = mean(ch_0_ampl);
ch_1_ampl_mean = mean(ch_1_ampl);
ch_0_ampl_offset = ch_0_ampl - ch_0_ampl_mean;
ch_1_ampl_offset = ch_1_ampl - ch_1_ampl_mean;
% Adjust time vector to start from 0 time_adj = time - time(1); % Subtract the first time value from all elements
% Create a new figure window showing the first figure
figure;
plot(time_adj, ch_1_ampl_offset, 'r', time_adj, ch_0_ampl_offset, 'b');
grid on;
title('Amplitude Offset for M1 and M2');
xlim([min(time_adj) max(time_adj)]);
xlabel('Time (s)');
ylabel('Amplitude Offset (V)');
legend('Microphone 1', 'Microphone 2');
[c, lag] = xcorr(ch_0_ampl_offset, ch_1_ampl_offset);
% Create new figure window showing cross-correlation graphs
figure;
plot(dtime * lag, c);
grid on;
title('Cross-Correlation between M1 and M2');
xlabel('Time Lag (s)');
ylabel('Cross-Correlation');
VS = 340; % speed of sound in ms^-1 [val, index] = max(c); time_diff = dtime * lag(index); delta_x = time_diff * VS; x_pos = (L - delta_x) / 2;
% Output calculation results disp(['Time Difference: ', num2str(time_diff), ' seconds']); disp(['Delta x: ', num2str(delta_x), ' meters']); disp(['Source Position: ', num2str(x_pos), ' meters']);
% Compute normalized cross-correlation [c_norm, lag_norm] = xcorr(ch_0_ampl_offset, ch_1_ampl_offset, 'coeff');
% Create a new graphics window to display the normalized cross-correlation graph
figure;
plot(dtime * lag_norm, c_norm);
grid on;
title('Normalized Cross-Correlation between M1 and M2');
xlabel('Time Lag (s)');
ylabel('Normalized Cross-Correlation');
% Find the maximum value of the normalized cross-correlation and calculate the time difference [val_norm, index_norm] = max(c_norm); time_diff_norm = dtime * lag_norm(index_norm);
% Output normalized calculation results disp(['Normalized Time Difference: ', num2str(time_diff_norm), ' seconds']);
2-Dimensional
ch_0 = load('C1Trace00001.dat');
ch_1 = load('C2Trace00041.dat');% trigger, reference
ch_2 = load('C4Trace00035.dat'); % Assuming filename and format
L = 2; % dist btw 2 microphones
c = 340; % speed of sound in ms^-1
time = ch_0(:, 1);
dtime = ch_0(2, 1)- ch_0(1, 1);
ch_0_ampl = ch_0(:, 2);
ch_1_ampl = ch_1(:, 2);
ch_0_ampl_mean = mean(ch_0_ampl);
ch_1_ampl_mean = mean(ch_1_ampl);
ch_0_ampl_offset = ch_0_ampl - ch_0_ampl_mean;
ch_1_ampl_offset = ch_1_ampl - ch_1_ampl_mean;
ch_2_ampl = ch_2(:, 2); ch_2_ampl_mean = mean(ch_2_ampl); ch_2_ampl_offset = ch_2_ampl - ch_2_ampl_mean;
% Adjust time vector to start from 0 time_adj = time - time(1); % Subtract the first time value from all elements
[c12, lag12] = xcorr(ch_0_ampl_offset, ch_1_ampl_offset); [c13, lag13] = xcorr(ch_0_ampl_offset, ch_2_ampl_offset); [c23, lag23] = xcorr(ch_1_ampl_offset, ch_2_ampl_offset);
[val12, index12] = max(c12); [val13, index13] = max(c13); [val23, index23] = max(c23);
Delta_t12 = dtime * lag12(index12); Delta_t13 = dtime * lag13(index13); Delta_t23 = dtime * lag23(index23); % Define the symbols syms R phi r = L / sqrt(3); % Distance from each microphone to the centroid of the triangle
eq1 = sqrt(R^2 + r^2 - 2*R*r*cos(phi + 2*pi/3)) - sqrt(R^2 + r^2 - 2*R*r*cos(2*pi/3 - phi)) == c * Delta_t12; eq2 = sqrt(R^2 + r^2 - 2*R*r*cos(phi)) - sqrt(R^2 + r^2 - 2*R*r*cos(phi + 2*pi/3)) == c * Delta_t13; eq3 = sqrt(R^2 + r^2 - 2*R*r*cos(2*pi/3 - phi)) - sqrt(R^2 + r^2 - 2*R*r*cos(phi)) == c * Delta_t23;
% Solve the system of equations [solution_R, solution_phi] = solve([eq1, eq2, eq3], [R, phi], 'Real', true); %[solution_R, solution_phi] = solve([eq2, eq3], [R, phi], 'Real', true);
% Calculate numerical solutions num_solution_R = vpa(solution_R); num_solution_phi = vpa(solution_phi);
% Display the solutions
disp('Solution for R:');
disp(num_solution_R);
disp('Solution for phi:');
disp(num_solution_phi);
Results
1-Dimensional
Relationship between time lags and theoretical locations
The inherent subjectivity of human observation often poses challenges in accurately determining the relative positions of sound waves, potentially leading to significant measurement errors. Consequently, reliance on the oscilloscope's direct reading of time differences (Δt) may yield results of questionable reliability.
The figure presented below delineates the relationship between the time lags and theoretical locations for four distinct types of sound sources. On the graph, three varieties of data markers are employed: squares denote the theoretical data points; circles correspond to manual readings; and triangles are indicative of the results computed by the code.
An intuitive assessment of the figure clarifies that the code-derived computational results exhibit markedly greater accuracy than those obtained through manual oscilloscope measurements. Utilizing the measured Δt, the position of the sound source can be calculated, which will be methodically analyzed in the subsequent section.
Relationship between calculated locations and theoretical locations
Clap
In our experiments, we first chose a single clap as the sound source. Multiple measurements were taken by clapping at locations between the two microphones, i.e., at 0, 50, 100, 150, and 200 cm, and the results are shown below.
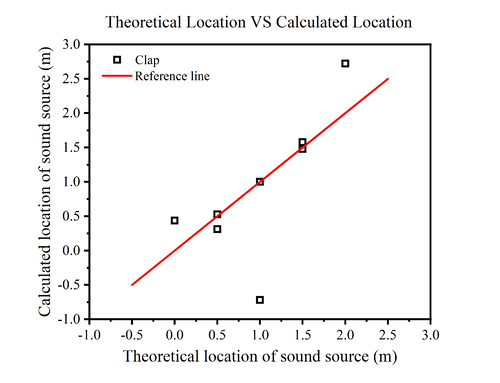 |
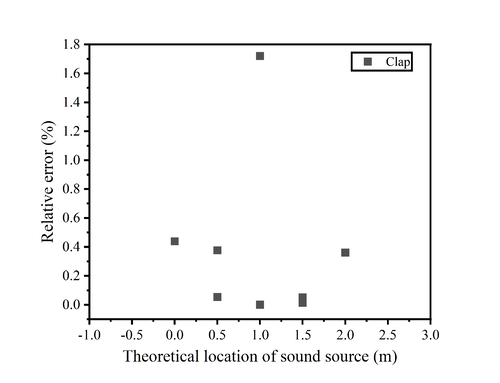 |
The figure shows the relationship between the theoretical position of the sound source and the calculated position. Since the horizontal coordinate is the theoretical position of the sound source, the vertical coordinate corresponding to the red straight line is the theoretical position of the sound source, so it is used as the reference line. The black square is the calculated sound source position.
Comparing the positions of the black square and the red line, it is found that the measurement error is larger at 0cm and 200cm (i.e., the positions of the two microphones), while the error is smaller at the position between the two microphones, and the closer to the midpoint of the two microphones, the closer to the theoretical position of the sound source is the calculated position of the sound source. One of the points fell farther below the reference line when the theoretical position was 1.0 m. It is speculated that this may be due to an operational error during the measurement process.
In order to better compare the error between the theoretical position and the calculated position, we calculated its relative error. From the figure, we can find that the relative errors of the measurements basically fall below 0.5% except for the one measurement that was operated incorrectly. The closer the sound source position is to the midpoint of the two microphones, the smaller the relative error is. When the sound source position is 1.0m, the relative error is only about 0.0005%, which almost indicates that the calculated position is the same as the theoretical position.
Speech Commands: 'Hello', 'A', 'Yes'
Due to the large error, we replaced the sound source with speech commands: 'Hello', 'A', 'Yes'. The experiment was repeated and the results obtained are shown in Fig.
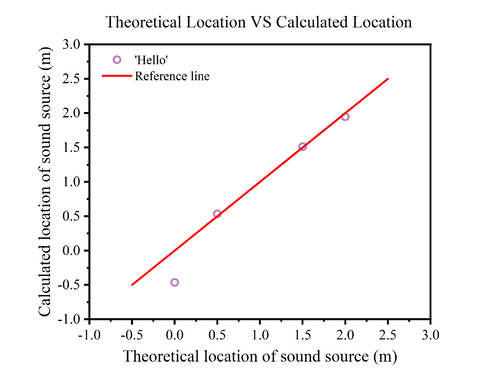 |
 |
 |
 |
In Fig.13(a), we replace the sound source with the speech command: 'hello', and we can find that the calculated position at 0cm has a large error with the theoretical position, while the remaining points are almost on the reference line. In Fig.13(c), the sound source is the speech command: 'A', four experiments were conducted at distances of 0.5m and 1.5m. It shows that the four calculated results closely align, and the theoretical positions are almost identical to the calculated positions.
It can be noticed that when we change the sound source from clapping to speech command, the error decreases. However, there is still a higher probability of error when the sound source is at both ends, while in the middle of the two microphones, our measurements and code calculations are able to call a more accurate location of the sound source.
The image of the relative error of 'hello' shows that only the measurement at 0cm has a large relative error of about 0.47%, while the rest of the measurements have a relative error of less than 0.1%. In contrast to the relative error produced by clapping, there is a significant reduction using the speech command. The image of the relative error of 'A' shows that the relative error of both measurements is 0.07% when the theoretical position is at 0.5m. When the theoretical position is at 1.5m, the relative error of both measurements is almost close to zero.
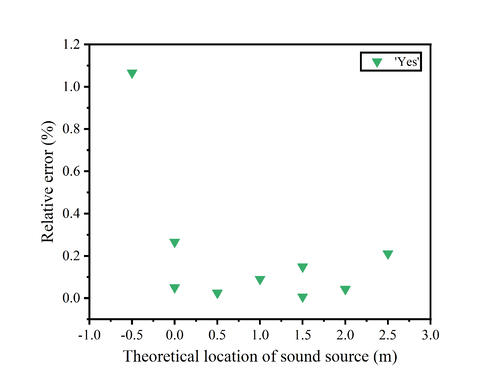
We also conducted several experiments when the sound source was 'yes', and in addition to measuring between the two microphones, we set the source at -50cm and 150cm for measurements.
 |
 |
One measurement at 0cm and another at 150cm produced errors, so we conducted a second experiment at the same location and obtained better results at both points. This shows that the determination of the sound source position may be subject to errors due to some accidental factors. Since we used a mobile phone to play a speech command, it is possible that the orientation of the mobile phone may have an effect on the results.
Also, we notice that when we set the sound at -50, 250cm, the calculated positions are almost at the theoretical positions of 0cm and 200cm. This is in accordance with the theory that, assuming the sound is at -50cm, the difference in time for the sound to reach the two microphones is exactly the time difference caused by the distance between the two microphones. Therefore, it is clear from the measurements that the device is not able to obtain the position of the sound source on the outside of the two microphones.
The relative error image of 'yes' reveals that one measurement at point 0 produces a large error of about 0.3%, while the rest of the measurements between 0-2.0m have a relative error of almost 0.15% or less. As we know from the previous description, it is not possible to determine the location of the sound source at the outside of the two microphones, so the relative error at the two points is larger, especially at -0.5m, where the relative error is about 1.1%.
Aggregate Sound Source Positioning
We have summarised all the measurements on a single graph in order to check the performance of the sensor more clearly.
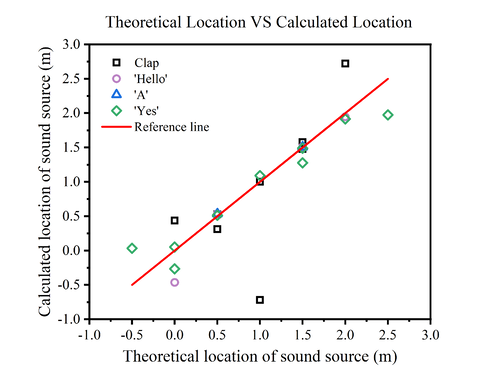 |
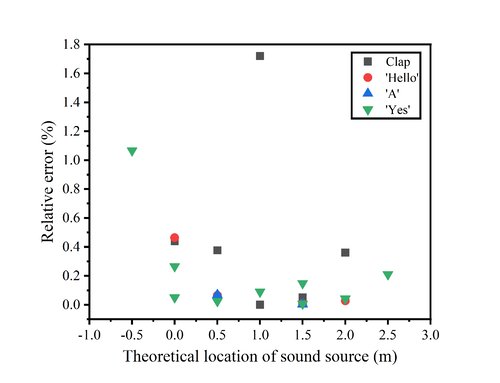 |
The figure shows the position measurements of the sensor for different sound sources at different locations. It can be noticed that the sensor performance is poorer and the error is larger when the sound is at the ends, and the closer the sound is to the midpoint of the two microphones, the smaller the measurement error is.
It is surmised that this may be because the closer the sound is to a particular microphone, the more sensitively variations can be reacted to this microphone. And when the sound is close to the middle, the resulting changes will be captured to the same extent by both microphones.
Clapping as a sound source may have a greater error than voice commands. This may be due to the fact that clapping sounds are more brief and sharp, which are less coherent and of short duration, making it difficult to extract precise temporal information from clapping sounds. Moreover, hand-clapping sounds contain a wide frequency range, including many high-frequency components, which may be subject to more attenuation and scattering during propagation, thus affecting measurement accuracy. On the contrary, voice commands have a long duration, a more regular and consistent acoustic pattern, a more concentrated frequency range, and a more stable acoustic signal.
In addition, there may be chance factors that affect the accuracy of the measurement, and multiple measurements may be required if accuracy is desired.
The relative error shows that excluding operational errors and measurements at -0.5m and 2.5m, we can keep the relative error below 0.5%, and even below 0.1% when the source is close to the midpoint of the two microphones. This shows that our sensor can accurately measure the position of the sound source in one dimension.
Error Analysis and Discussions
In the process of sound source localization using cross-correlation techniques in MATLAB, various factors can introduce significant errors. These include human-induced errors during operation and readings, as well as the intrinsic limitations of the `xcorr` function.
Human factors
- Optimal Parameter Settings:
- Finding the most accurate setting for measurement parameters is crucial. Incorrect settings can lead to insufficient precision, significantly impacting the calculated results and the actual sound source location.
- Time Division Settings: Larger time divisions may produce sharper peaks but decrease time precision, affecting overall location accuracy. Conversely, smaller divisions can increase precision but limit the measurable sound duration.
- Voltage Division Settings: The ratio of the sound wave to the oscilloscope display scale must be optimally set to ensure that waveforms are neither too compressed nor too elongated, as both extremes can distort correlation accuracy.
Limitations of Cross-Correlation (xcorr)
- Sampling Frequency and Data Point Quantity:
- Sampling Rate and Data Points: The accuracy of the time delay measured by the cross-correlation function (`xcorr`) is contingent upon the sampling rate and the number of data points.
- If the sampling interval is too large or if the signal is not continuously recorded, the time delay derived may not be very precise.
- Higher sampling rates can provide more detailed data and potentially more accurate delay estimates.
- Sampling Rate and Data Points: The accuracy of the time delay measured by the cross-correlation function (`xcorr`) is contingent upon the sampling rate and the number of data points.
- Signal Characteristics and Noise:
- Waveform Integrity and Noise: An incomplete waveform or significant noise within the signal can lead to erroneous interpretations by the cross-correlation algorithm.
- Low-frequency oscillations or small amplitude variations can make it difficult for `xcorr` to accurately identify the delay corresponding to the peak correlation.
- Ensuring high signal integrity and minimizing noise are crucial for reliable cross-correlation analysis.
- Sound Signal Attenuation: The natural decay of the sound signal with distance may influence the code's ability to judge and compare waveforms accurately.
- Sound intensity diminishes as it travels through the medium, which could lead to variations in the recorded waveforms at different distances.
- Waveform Integrity and Noise: An incomplete waveform or significant noise within the signal can lead to erroneous interpretations by the cross-correlation algorithm.
- Boundary Effects and Window Size:
- Effects of Signal Length and Window Size: The outcome of cross-correlation analysis is also influenced by the length of the signal and the size of the processing window.
- Short signals or inappropriate window sizes can lead to misinterpretation of delays, affecting the overall results.
- Adjusting the window size to adequately capture the dynamics of the signal without truncating important features is essential.
- Effects of Signal Length and Window Size: The outcome of cross-correlation analysis is also influenced by the length of the signal and the size of the processing window.
It is imperative to meticulously consider and, where possible, quantify each potential source of error. By doing so, the interpretation of data can be significantly enhanced, improving the reliability of the sound source localization methodology.
Possibility of improvement
Improvement of experimental equipment
In order to improve the accuracy and repeatability of sound detection when the equipment is more fragmented and lacks a complete automation system, the following is an expanded description for each aspect:
- Fixed microphone position: Design and implement a stand or shelf to fix the microphone in a suitable position to ensure that the distance between them is always consistent.
- Noise control: In order to reduce the noise that may be introduced, a number of measures can be taken. Place the experimental equipment in a relatively quiet environment, away from sources that may produce noise. Or use sound insulation materials such as foam or sponge board to isolate the sound source, and arrange sound insulation materials around the microphone to absorb ambient noise.
- Replace more advanced experimental equipment : Consider updating the microphone sensor and oscilloscope in the equipment to a more advanced model. Choose a microphone sensor with higher sensitivity and a wider frequency response range to ensure that you can capture a more accurate and rich sound signal. Through the use of advanced equipment, the quality and accuracy of sound data can be significantly improved, thus enhancing the credibility and repeatability of experimental results.
Algorithm improvement
- Code Efficiency: Preallocate memory for large matrices as we know their size beforehand to improve performance. For loops that can be vectorized, do so to utilize MATLAB’s optimized matrix operations.
- Code Modularity: Consider breaking it into functions or scripts for better reuse and modularity.
Others
In order to make the device more multi-functional and intelligent, and more practical prospects, the following functions can be considered:
- Specific voice recognition: Integrated speech recognition software or algorithms allow the device to recognize specific voice patterns or frequencies. This capability can be used by training the model to recognize specific sounds, such as a specific command, the sound of a specific object, or noises common in the environment. By identifying specific sounds, such as those coming from different directions or specific locations, it is possible to infer the direction or location from which the sound may have come. For example, if the device is able to recognize that a particular sound pattern is coming from the left and another particular sound pattern is coming from the right, their relative positions can be inferred. Recognizing a particular sound, the device can take preset actions, such as triggering an alarm, recording data, or executing specific control commands. Such a function can improve the intelligence level of the device and make it more suitable for various application scenarios.
- Sound analysis function: The device can have sound analysis function for in-depth analysis of sound spectrum, intensity and other information. Through a more detailed analysis of the sound, the source, type and characteristics of the sound can be identified. The sound characteristics provided by the sound analysis function also help further identify the source and location of the sound. Therefore, the recognition of specific sounds and the analysis of sounds can provide important auxiliary information for sound location, thus enhancing the positioning accuracy and reliability of the device.
Logs
Build a link to record experiment log. Please click me!!!
References
- 2D theory: https://patentimages.storage.googleapis.com/a9/99/44/a66234cb68ab63/CN103995252B.pdf
- 3D theory: https://patentimages.storage.googleapis.com/7d/26/47/a6bce6afc723c6/CN103064061B.pdf
- Microphone datasheet: https://cdn-learn.adafruit.com/downloads/pdf/adafruit-agc-electret-microphone-amplifier-max9814.pdf
- Oscilloscope datasheet: https://www.testequipmenthq.com/datasheets/LECROY-WAVESURFER%2064XS-Datasheet.pdf
- TDOA theory: https://iot-book.github.io/13_%E6%97%A0%E7%BA%BF%E5%AE%9A%E4%BD%8D/S2_TDOA%E5%AE%9A%E4%BD%8D%E7%AE%97%E6%B3%95/
Sensor that recognizes specific sounds and steers toward the source
This is the name and link of the previous page. We adjusted the final project name displayed on the main page based on the final results and conditions.






























![{\displaystyle ={\frac {1}{2(d_{2}-d_{1})}}[(d_{2}-d_{1})^{2}-d_{1}^{2}+d_{2}^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86b60c57298e3f82cc58ac7f7d55f95f47bc783b)
![{\displaystyle ={\frac {1}{2C\cdot \Delta t_{21}}}[(C\cdot \Delta t_{21})^{2}+2xd_{1}-d_{1}^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaa37d8a4a67420791129007bff96e0783eb4f76)
![{\displaystyle {\sqrt {x^{2}+y^{2}+z^{2}}}=d_{2}={\frac {1}{2C\cdot \Delta t_{23}}}\left[(C\cdot \Delta t_{23})^{2}+2dy-d^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb769f42a477223503f51a40a7c97510b486dd02)
![{\displaystyle {\sqrt {(x-D)^{2}+y^{2}+z^{2}}}=d_{4}={\frac {1}{2C\cdot \Delta t_{45}}}\left[(C\cdot \Delta t_{45})^{2}-2dx(x-D)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06cd26b0603615801c2570ee735ec7d57f1dbc73)
![{\displaystyle {\sqrt {(x-D)^{2}+y^{2}+z^{2}}}=d_{4}={\frac {1}{2C\cdot \Delta t_{46}}}\left[(C\cdot \Delta t_{46})^{2}+2Dx+D^{2}-2dy-d^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/349796896668dc3b3bb498dbfd3c71fe72513e2f)