Quartz Crystal MicroBalance (QCM)

Abstract

This project aims to construct a circuit that mimics a quartz crystal microbalance. This can be done via a combination of resistors, capacitors, and a quartz crystal. Testing of the QCM can be done by measuring the fundamental frequency of the quartz crystal oscillator, followed by adding a test mass such as the ink of a permanent marker on the oscillator to determine the frequency change. The original intention of building this QCM is to investigate if it is possible to measure the mass of thin films ex-situ. However, due to experimental and time constraints, we shall focus on building a circuit that can detect mass changes on the order of micrograms.

Team members

Tan Jhoon Yong

Idea

Quartz crystal microbalance (QCM) is widely used to measure mass changes to substances involved in physical and chemical processes. In my field of research, we often have to find out the thicknesses of thin films as part of the process of characterizing the samples. There are a few methods that are usually employed in my research to measure thin films' thicknesses such as observing the reflection high-energy electron diffraction (RHEED) oscillations during pulsed-laser deposition (PLD), atomic force microscopy (AFM), X-ray diffraction (XRD) (if the sample is ordered), and fitting of data from spectroscopic ellipsometry (SE). These techniques usually expend a significant amount of time but provide an accurate value to the thickness measurements. Creating a QCM that can work ex-situ will assist my research, and also serves as a reference point and hastens the process of fitting models in SE analysis.

Many of the developments and features that exist in today’s commercial QCM instruments were pioneered in laboratories with custom-built instruments to meet specific research needs, such as the use of internal reference crystals to separate the effects of a liquid environment from those of a film sample.

Sample Preparation

7 samples of varying thicknesses of Au are deposited on a 10mm x 10mm x 0.5mm MgO(001) substrate using magnetron sputtering in an Ar-filled chamber. Insitu thickness measurement results are as follows: 20.6nm, 12.4nm, 8.3nm, 4.2nm, 2.1nm, 1.0nm.

Working Principle

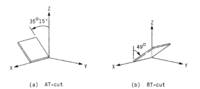
The working principle behind the QCM is based on the piezoelectric effect. The piezoelectric effect is the generation of electric charges by a crystalline material upon subjecting it to stress.[1] An oscillating electric field applied across the device induces an acoustic wave that propagates through the crystal and meets minimum impedance when the device's thickness is a half-integer multiple of the wavelength of the acoustic wave.[2] It is a shear mode device in which the acoustic wave propagates in a direction perpendicular to the crystal surface.[3] Therefore, crystals cut in specific crystal axes have to be used to utilize the shear mode.

A resonant oscillation in the crystal is achieved by putting the crystal in an oscillation circuit where the electrical and mechanical oscillations are close to the fundamental frequency of the crystal. Changes to the mass of the crystal would result in a proportional change in its natural frequency according to the Sauerbrey equation[4]

$\Delta m={\frac {C}{n}}\Delta f$

where $\Delta f$ is the change in resonance frequency, $C$ is the specific sensitivity of the crystal, $\Delta m$ is the mass adsorbed on the active area, and $n$ is the harmonic number. $C$ describes how much material per unit area is required to change the resonant frequency of the crystal by 1Hz. A smaller $C$ value gives a higher mass sensitivity. This value depends on the fundamental resonant frequency of the crystal, and it is defined as

$C={\frac {t_{q}\rho _{q}}{f_{0}}}$

where $t_{q}$ is the thickness of the quartz, $\rho _{q}$ is the density of the quartz plate, and f₀ is the fundamental resonant frequency of quartz. With these, we can determine the mass of the deposited material.

Another consideration would be the energy dissipation of the crystal to the surroundings. This is important, especially for viscoelastic films. Viscoelastic films violate the Sauerbrey condition that the bound mass is rigidly attached to the crystal without any slip. Such viscoelastic films dissipate energy via mechanical losses in the flexible mass.

Orientation of AT- and BT- cut crystals

Setup

The typical QCM set-up of piezoelectric quartz crystal microbalance is shown in Figure (). The oscillator circuit is connected to the power supply and sample stage mount where the piezoelectric quartz crystal is. We can determine the resonance frequency of the quartz crystal using an oscilloscope, frequency counter, or spectrum analyzer. To determine the feasibility of this QCM project, we built a simple oscillating circuit as a foundation to test if we can detect the resonance frequency of the quartz crystal. This also serves as a time buffer while waiting for the AT-cut quartz to be delivered. Figure () shows the electrical circuit diagram and its implementation on a breadboard. As the electrical current generated from the oscillation of the quartz crystal is an alternating current due to the piezoelectric effect, we employ the usage of logic gates called inverters to convert DC to AC for readout. Adding a resistor to the circuit allows for the control of the potential difference across the inverter. In this oscillating circuit, we use a 14-pin integrated circuit and measure the resonant frequency of a CMAC CK q5 crystal oscillator.

Measurements

....

References

1. Meissner A (1927) € Uber piezoelectrische Krystalle bei Hochfrequenz. Z Tech Phys 8:74
2. O’Sullivan, C. K., & Guilbault, G. G. (1999). Commercial quartz crystal microbalances – theory and applications. Biosensors and Bioelectronics, 14(8), 663–670.
3. Ebersole, R., Miller, J., Moran, J., & Ward, M. (1990). PZ quartz sensors for use in clinical analysis. J. Am. Chem. Soc, 112, 3239.
4. Sauerbrey, G. (1959). Verwendung von Schwingquarzen zur Wägung dünner Schichten und zur Mikrowägung. Zeitschrift für Physik, 155(2), 206–222.