Optical Sensor for Noise Flickering: Difference between revisions
No edit summary |
|||
| Line 176: | Line 176: | ||
===Internal Capacitance=== | ===Internal Capacitance=== | ||
The time constant of the photodiode | The time constants for red and blue LEDs with different external resistance are determined experimentally. The time constant is related to the internal capacitance of the photodiode through the following equation, | ||
𝜏 = RC | |||
in which 𝜏 is the time constant, R is the external resistance, and C is the internal capacitance. From experimental results, the internal capacitance is calculated and shown in the table below. | |||
{| class="wikitable" style="margin:auto" | | |||
! LED !! Resistance (Ω) !! Time constant (ms) !! Internal Capacitance (nF) | |||
|- | |||
| Red || 10k || N.A. || N.A. | |||
|- | |||
| || 100k || 0.02 || 0.2 | |||
|- | |||
| || 1M || 0.07|| 0.07 | |||
|- | |||
| Blue || 10k|| N.A. || N.A. | |||
| || 100k|| 0.05 || 0.5 | |||
| || 1M|| 0.09 || 0.09 | |||
|} | |||
===Other Light Source(s)=== | ===Other Light Source(s)=== | ||
Revision as of 23:56, 10 April 2024
Group Members
Eric Cheung Jun Hao; Lee An Min, Amanda; Loh Jia Ying Whitney
Background and Introduction
The objective of this project is to characterise a given photodiode and to successfully determine the frequency of an unknown flickering light source.
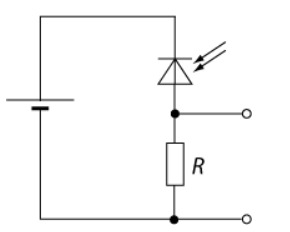
With a simple potential divider, consisting a resistor and a photodiode in series, the resistance and hence sensitivity of the photodiode can be determined. By exposing the photodiode to visual noise tags, such as the flickering of LEDs, the resistance across the photodiode is expected to decrease and hence, a larger potential can be measured across the resistor. The photodiode resistance is a function of light exposure. The resistance is inversely proportional to light intensity. The output can be observed on an oscilloscope to determine the performance of the photodiode.
Set-Up
Equipment Needed
| S/N | Item | Description/Model No. |
|---|---|---|
| 1 | Soldering Iron | - |
| 2 | Soldering Tin | - |
| 3 | Wires | - |
| 4 | Resistors | 10k, 100k, 1M |
| 5 | Photodiode | Hamamatsu S5972 |
| 6 | DC Power Supply | Matrix MPS-3005L-3 |
| 7 | Signal Generator | Agilent 33220A |
| 8 | 2GHz Digital Oscilloscope | LeCroy WaveRunner 203MXi-A |
| LED S/N | Colour | Wavelength (nm) | Size (mm) |
|---|---|---|---|
| 1 | Red | 643 | 5 |
| 2 | Amber | 605 | 5 |
| 3 | Green | 570 | 5 |
| 4 | Blue | 450-495 | 5 |
Experimental Set-up
Characterization of the photodiode is done with three 5 mm LEDs: (i) red, 643nm; (ii) green, 570nm; and (iii) blue, 450nm to 495nm. It can be noted that the photodiode sensitivity increases with increasing wavelength of LED used.
The photodiode used in this experiment is Hamamatsu S5972 Si PIN photodiode. According to the datasheet, it has a spectral response range between 320nm to 1000nm, with a peak sensitivity at 800nm, near infrared radiation. The cutoff frequency is 0.5GHz at reverse bias of 10V. The terminal capacitance at reverse bias of 2V is close to 3pF.
A signal generator is used to pulse the LEDs to create a flickering light source. A square wave with a peak-to-peak voltage of 2V is used across all the measurements taken. A DC power supply is used to supply 3V across the photodiode.
The performance of the photodiode will be determined by varying the following parameters: (i) wavelength of LED; (ii) external resistor in circuit; and (iii) frequency of LED blinking (1Hz - 100kHz).
The dependent variable that will be measured is the voltage reading across external resistor
This will allow us to determine the following parameters (i) response of photodiode at different wavelengths; (ii) efficiency (Time decay) of photodiode at different wavelengths; and (iii) internal capacitance (time constant) of photodiode.
Timeline and Milestone
| Week | Dates | Tasks |
|---|---|---|
| Week 7 | 4 - 8 Mar | Collecting equipment and prelimary set-up |
| Week 8 | 11 - 15 Mar | Complete circuit set-up and prelimary measurements |
| Week 9 | 18 - 22 Mar | Data collection (vary LEDs) |
| Week 10 | 25 - 29 Mar [Well-being day (28 Mar), Good Friday (29 Mar)] | Data collection (vary resistance) |
| Week 11 | 1 - 5 Apr | Data Analysis and further measurements (if needed) |
| Week 12 | 8 - 12 Apr [Hari Raya (10 Apr)] | Data Analysis and explore other light sources (phone/computer screens) |
| Week 13 | 15 - 19 Apr | Analyse experimental results and complete documentation |
Results
Varying External Resistance
Relationship between resistance and cut-off frequency
It can be concluded that as external resistance increases, the cutoff frequency decreases. Decreasing the external resistance by one order of magnitude will increase the cut-off frequency by an order of magnitude. Hence, lower resistance needs to be used in order to measure at higher frequencies.
Comparing the results for red LED,
| Resistance (Ω) | Cutoff Frequency (kHz) | Reasoning |
|---|---|---|
| 10k | 100 | Graphically, the voltage across the external resistor can reach and maintain at a steady-state value when f=10kHz but not at 100kHz. Based on a rise time of approximately 0.01ms, the cutoff frequency can be estimated to be close to 100kHz. |
| 100k | 33 | Graphically, the voltage across the external resistor can reach and maintain at a steady-state value when f=10kHz but not at 100kHz. Based on a rise time of approximately 0.03ms, the cutoff frequency can be estimated to be close to 30kHz. |
| 1M | 6 | Graphically, the voltage across the external resistor can reach and maintain at a steady-state value when f=1kHz but not at 10kHz. Based on a rise time of approximately 0.15ms, the cutoff frequency can be estimated to be close to 7kHz. |
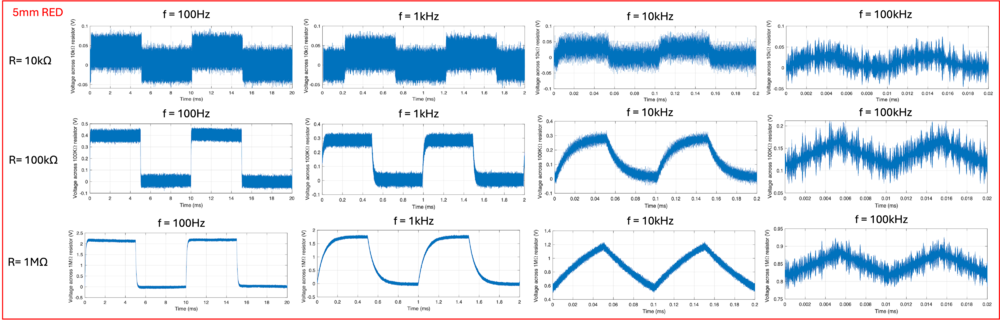
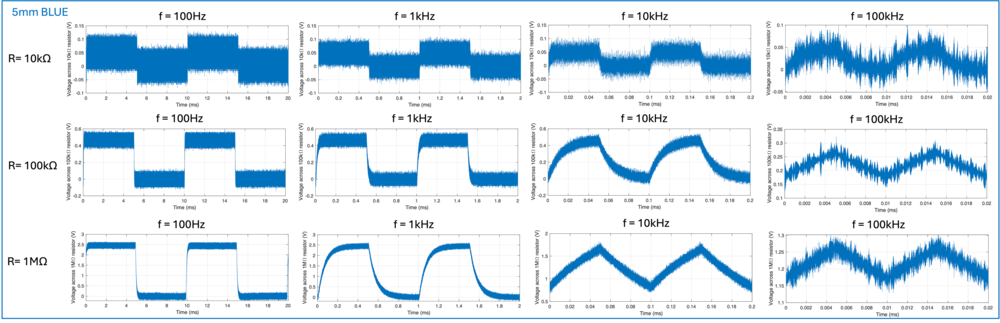
Repeating the same analysis for the blue LED,
| Resistance (Ω) | Cutoff Frequency (kHz) | Reasoning |
|---|---|---|
| 10k | 500 | Graphically, the voltage across the external resistor can reach and maintain at a steady-state value when f=10kHz but not at 100kHz. Based on a rise time of approximately 0.003ms, the cutoff frequency can be estimated to be ~300kHz. |
| 100k | 14 | Graphically, the voltage across the external resistor can reach and maintain at a steady-state value when f=10kHz but not at 100kHz. Based on a rise time of approximately 0.04ms, the cutoff frequency can be estimated to be ~25kHz. |
| 1M | 6 | Graphically, the voltage across the external resistor can reach and maintain at a steady-state value when f=1kHz but not at 10kHz. Based on a rise time of approximately 0.20ms, the cutoff frequency can be estimated to be close to 5kHz. |
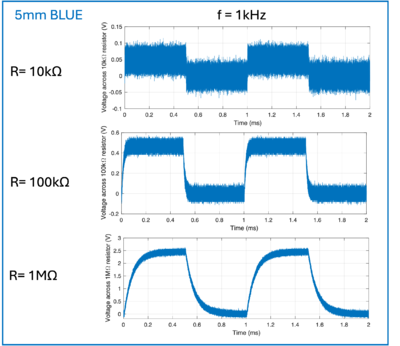
Narrowing down to the specific frequency of 1kHz for blue LED for a clearer illustration, it can be shown that with decreasing external resistance, time constant decreases which replicates the signal sent into the LED (square wave). However, a lower resistance will entail lower signal-to-noise ratio. At the lower resistance of 10kΩ, the signal captured resembles a square wave while the higher resistance of 1MΩ shows, there is an evident decay in the rise and fall of the captured signal. Furthermore, the graphs also illustrate that the background noise is more prominent at lower resistance as the steady-state value across the lower resistance is smaller.
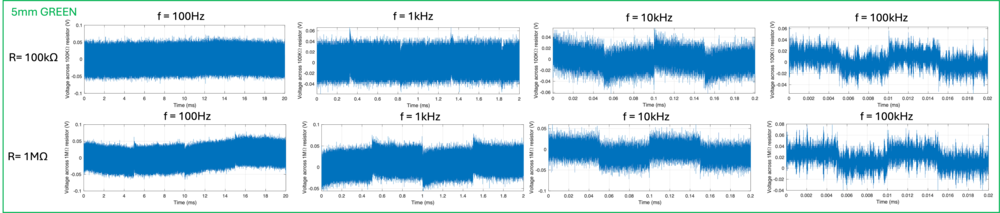
For completeness of our discussion, the plots obtained from the measurements of the green LED is shown below. However, due to the low steady-state value of the voltage across the resistor, the rise time of the photodiode cannot be clearly determined.
Varying Wavelength
From our experimental results, the photodiode has a faster response at longer wavelengths.
| LED | Wavelength (nm) | Resistance (Ω) | Rise Time (ms) | Remarks |
|---|---|---|---|---|
| Red | 643 | 10k | 0.01 | |
| 100k | 0.03 | |||
| 1M | 0.16 | |||
| Green | 570 | 10k, 100k, 1M | N.A. | Low signal-to-noise ratio |
| Blue | 450-495 | 10k | 0.002 | |
| 100k | 0.07 | |||
| 1M | 0.18 |
Out of the three LEDs used, the signal-to-noise ratio of the green LED is the lowest. Powering the three LEDs reveals that with the same voltage supplied, the green LED is the dimmest. Thus, the intensity of incident green light on the photodiode is significantly lower. The signal captured by the photodiode is lower and hence, the decrease in resistance of the photodiode is smaller. As a result, the voltage across the external resistor in the circuit of a fixed resistance is lower. Because of this, the change in voltage reading (in the switching of the LED) on the oscilloscope is closer to background noise. Thus, signal-to-noise ratio is lower.

Considering LEDs flickering at 100Hz, the following steady-state values for voltage across the external resistor were obtained.
For the Red LED,
| Resistance (Ω) | Steady State Value (V) |
|---|---|
| 10k | 0.04 |
| 100k | 0.40 |
| 1M | 2.15 |
For the Blue LED,
| Resistance (Ω) | Steady State Value (V) |
|---|---|
| 10k | 0.05 |
| 100k | 0.50 |
| 1M | 2.45 |
The steady-state value is dependent on the photosensitivity at different wavelengths and the brightness of the LED.
Internal Capacitance
The time constants for red and blue LEDs with different external resistance are determined experimentally. The time constant is related to the internal capacitance of the photodiode through the following equation,
𝜏 = RC
in which 𝜏 is the time constant, R is the external resistance, and C is the internal capacitance. From experimental results, the internal capacitance is calculated and shown in the table below.
| LED | Resistance (Ω) | Time constant (ms) | Internal Capacitance (nF) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Red | 10k | N.A. | N.A. | ||||||||
| 100k | 0.02 | 0.2 | |||||||||
| 1M | 0.07 | 0.07 | |||||||||
| Blue | 10k | N.A. | N.A. | 100k | 0.05 | 0.5 | 1M | 0.09 | 0.09 |
Other Light Source(s)
The photodiode is used to characterise the flickering of a white computer screen.