High Sensitive Position Sensor based on PDH technique

Team members

Angela Anna Baiju and Chenyue Gu

Idea

This project is aiming of using Pound–Drever–Hall (PDH) technique to sense the vibration and the movement of the mirror driven by the noise from the environment (acoustic, thermal, etc.).

Pound–Drever–Hall laser frequency stabilisation is a powerful technique providing a means to stabilise the frequency of a laser to a specific reference frequency. It is commonly employed in precision measurements and experimental setups where precise control over the laser frequency is required, such as interferometric gravitational-wave detector. Alternatively, if a stable laser is available, the PDH technique can be used to stabilise and/or measure the instabilities in an optical cavity length via the error signal readout from the cavity.

In this project, we will lock the cavity by reading the error signal of reflection/transmission of the cavity and then feed it back to the input mirror, moving the mirror with a PZT. And then we can read out the cavity length change from the error signal. This sensing technique is commonly using in LIGO-Virgo-KAGRA (LVK) interferometric gravitational wave detection community, as well as quantum optomechnics.

Pound-Drever-Hall Method

The idea behind the PDH method is simple: A laser’s frequency is measured with a Fabry–Perot cavity, either transmission or reflection, and then is fed back to the input laser to suppress frequency fluctuations. The process begins with modulating the laser light. This is typically achieved by imposing a high-frequency (radio frequency or microwave) signal onto the laser beam (Local Oscillator). This modulation creates sidebands around the carrier frequency of the laser light. These sidebands are symmetrically spaced around the carrier frequency. The modulated laser light then passes through an electro-optic modulator (EOM). The EOM applies phase modulation to the light, causing the sidebands to shift in frequency relative to the carrier frequency. The amount of phase modulation applied determines the frequency separation between the carrier and the sidebands. The phase-modulated laser light is directed onto a frequency reference, which can be a stable Fabry–Perot cavity. The reflected beam is then picked off and compared with the local oscillator's signal via a mixer whose output is the product of its inputs. From the output of the mixer, by using a low-pass filter, the dc (or very low frequency) part which is of interest remains and the ac (or high frequency) part that is usually the twice the modulation frequency is filtered out. The remaining dc signal, so called error signal, then goes through the feedback loop. The feedback loop typically involves a control mechanism, such as adjusting the current supplied to the laser diode or controlling the frequency of the modulation signal. The feedback loop aims to minimise the error signal by stabilising the laser frequency to match the reference frequency. A basic setup of PDH method is shown in Fig. 1 .

Fig. 1 A basic diagram of the setup implementing Pound-Drever-Hall method. In this digram, the laser frequency is modulated with a Pockels cell, driven by some local oscillator. The reflected beam is picked off with an optical isolator (a polarising beamsplitter and a quarter-wave plate makes a good isolator) and sent into a photodetector, whose output is compared with the local oscillator’s signal via a mixer. A low-pass filter on the output of the mixer isolates this low frequency signal, which then goes through a servo am- plifier and into the tuning port on the laser, locking the laser to the cavity. The Faraday isolator keeps the reflected beam from getting back into the laser and destabilizing it.

To implement the method, we need to know well about how to process the error signal, which is the heart of the technique. We follow the derive from Eric D. Black's paper , and run simulation by Python.

Reflection of a monochromatic beam from a Fabry-Perot cavity

To start the math behind it, we pick a point outside the cavity and measure the electric field over time. Then the magnitude of the electric field of the incident and the reflected beams can be written as

$E_{in}=E_{0}e^{i\omega t}$,

$E_{re}=E_{1}e^{i\omega t}$,

where $\omega$ is the incident laser frequency, $E_{0}$ and $E_{1}$ are complex, and in this way, we account for the relative phase between the two waves in. The reflection coefficient $F(\omega )$ is thus given by

$F(\omega )=E_{re}/E_{in}={\frac {r\left(e^{i{\frac {\omega }{\Delta \nu _{FSR}}}}-1\right)}{1-r^{2}e^{i{\frac {\omega }{\Delta \nu _{FSR}}}}}}$.

Here we consider a lossless and symmetric Fabry-Perot cavity formed with two mirrors whose amplitude reflection coefficient are both $r$. The free spectral range of the cavity is denoted as $\Delta \nu _{FSR}=c/2L$.

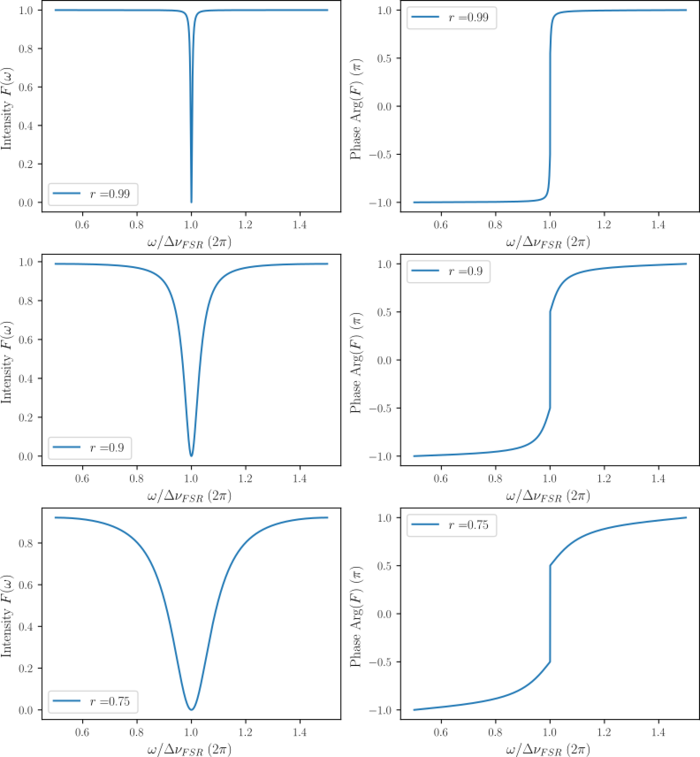
Fig. 2 Magnitude and phase of the reflection coefficient for a Fabry-Perot cavity. The finesse is different for the figure of different rows. According to different $r=0.99,0.90,0.75$, from the top row the the bottom row, the figures show the reflection coefficient for cavities of fitness equals to $312.58$, $29.80$, and $10.88$ respectively. Note the discontinuity in phase (the straight line around $\omega /\Delta \nu _{FSR}=2\pi$), caused by the reflected power vanishing at resonance.

Noted that $F(\omega +2\pi n\Delta \nu _{FSR})=F(\omega )$, so the cavity has infinite resonant frequencies at $\omega _{c}=2\pi n\Delta \nu _{FSR}$ (where $n$ is an integer), and here we just plot the reflection coefficient around one cavity resonance as an example.

Modulating the beam: sidebands and the error signal

As shown in figure 2, when the frequency of the incident beam is detuned away from the resonance ($\omega /\Delta \nu _{FSR}>2n\pi$ or $\omega /\Delta \nu _{FSR}<2n\pi$), one can not tell the difference between blue- (higher frequency) and red-(lower frequency) detuning by looking at the magnitude (intensity) of the reflection coefficient. This is because the magnitude of the reflection coefficient is symmetric about the cavity resonant frequency. However, the phase profile near the resonance does not have this feature. Instead, it has a huge change and is discontinuous. Thus, to tell whether the laser's frequency is above or below the cavity resonance, we need to measure the phase of the reflected beam. In order to do so, we need to modulate the beam and generate sidebands with a definite phase relationship to the incident and reflected beams. After interfering these sidebands with the reflected beam, we will get a beat pattern at the modulation frequency, which gives the information of the phase of the reflected beam.

Creating the sidebands

Now, we apply a phase modulation on the input field, and we can write its electric field as

$E_{in}=E_{0}e^{i(\omega t+\beta sin\Omega t)}$,

where $\Omega$ is the modulation frequency, and $\beta$ is the modulation depth. Thus, we can write the expansion of this expression with Bessel function as

$E_{in}\approx \left[J_{0}(\beta )+2iJ_{1}(\beta )sin\Omega t\right]e^{i\omega t}=E_{0}\left[J_{0}(\beta )e^{i\omega t}+J_{1}(\beta )e^{i(\omega +\Omega )t}-J_{1}(\beta )e^{i(\omega -\Omega )t}\right]$.

It shows that after the modulation, there are actually three different beams incident on the cavity: a carrier with angular frequency of $\omega$ and two sidebands with frequencies of $\omega \pm \Omega$. And if we denote the total power of the incident beam as $P_{0}\equiv |E_{0}|^{2}$, the power of the carrier and the first-order sidebands can be written as

$P_{c}=J_{0}^{2}(\beta )P_{0}$,

$P_{s}=J_{1}^{2}(\beta )P_{0}$.

With a small modulation depth ($\beta <1$), we can assume all the power is in the carrier and the first-order sidebands ($P_{c}+2P_{s}\approx P_{0}$).

Measuring the error signal

After modulation, the total reflection is written as the sum of the reflection of the carrier and two sidebands

$E_{re}=E_{0}\left[F(\omega )J_{0}(\beta )e^{i\omega t}+F(\omega +\Omega )J_{1}(\beta )e^{i(\omega +\Omega )t}-F(\omega -\Omega )J_{1}(\beta )e^{i(\omega -\Omega )t}\right]$

And the power of the reflected beam can then be obtained as

$P_{re}=|E_{re}|^{2}=P_{c}|F(\omega )|^{2}+P_{s}\left[|F(\omega +\Omega )|^{2}+|F(\omega -\Omega )|^{2}\right]$

$~~+2{\sqrt {P_{c}P_{s}}}\left[{\mathcal {Re}}\left(F(\omega )F^{*}(\omega +\Omega )-F^{*}(\omega )F(\omega -\Omega )\right)cos\Omega t+{\mathcal {Im}}\left(F(\omega )F^{*}(\omega +\Omega )-F^{*}(\omega )F(\omega -\Omega )\right)sin\Omega t\right]$

$~~~+(2\Omega ~term)$,

where we show the production of the three different frequencies, the carrier at $\omega$ and the upper and the lower sidebands at $\omega \pm \Omega$. We ignored the $2\Omega$ term which comes from the sidebands interfering with each other.

As shown in the equation, we get dc components related to the carrier and the two sidebands frequencies, and a sine term and a cosine term oscillating at the modulation frequency. We are interested in the oscillating terms because they carry the information of the phase of the reflected carrier. And we will see in the following, usually, at low modulation frequencies only the cosine term survives, and at high modulation frequencies, only the sine term is important.

Now we multiply the reflection signal with the modulation frequency ($sin\Omega t$) with a mixer, we get

$P_{mix}=P_{re}sin\Omega t=P_{I}+P_{dc}sin\Omega t-{\frac {1}{2}}P_{I}cos2\Omega t$,

where

$P_{dc}=P_{c}|F(\omega )|^{2}+P_{s}\left[|F(\omega +\Omega )|^{2}+|F(\omega -\Omega )|^{2}\right]$,

$P_{I}=2{\sqrt {P_{c}P_{s}}}{\mathcal {Im}}\left(F(\omega )F^{*}(\omega +\Omega )-F^{*}(\omega )F(\omega -\Omega )\right)$,

and we see in the mixed signal, the cosine term in the reflection is totally vanished. So in order to gain the information from the cosine term, we need to turn the sine signal into a cosine signal, so we can simply adding $\pi /2$ a phase shift, which can we achieved by a phase shifter or a delay line.

Then we will get

$P_{mix}=P_{re}cos\Omega t=P_{R}+P_{dc}cos\Omega t+{\frac {1}{2}}P_{R}cos2\Omega t$,

where

$P_{R}=2{\sqrt {P_{c}P_{s}}}{\mathcal {Re}}\left(F(\omega )F^{*}(\omega +\Omega )-F^{*}(\omega )F(\omega -\Omega )\right)$.

After the mixer, the information in the cosine and sine terms in the reflection signal are now become the only dc signal in the mixed signal. Then we can isolate them with a low-pass filter.

Fast modulation near resonance

In the regime when the carrier is near resonance and the modulation frequency is high enough ($\Omega \gg \Delta \nu _{FSR}/{\mathcal {F}}$) that the sidebands are not, we can assume that the sidebands are totally reflected that $F(\omega \pm \Omega )\approx -1$. Thus

$F(\omega )F^{*}(\omega +\Omega )-F^{*}(\omega )F(\omega -\Omega )\approx -i2{\mathcal {Im}}[F(\omega )]$,

is purely imaginary. In this regime, we mixed the reflection signal with the in-phase modulation signal and get the error signal as

$\epsilon =P_{I}=2{\sqrt {P_{c}P_{s}}}{\mathcal {Im}}\left(F(\omega )F^{*}(\omega +\Omega )-F^{*}(\omega )F(\omega -\Omega )\right)$.

Figure 3 shows a plot of this error signal.

Figure 3. Error signal with high frequency modulation. From left to right, the figures show the error signal for cavities of fitness equals to $312.58$, $29.80$, and $10.88$ respectively.

Slow modulation

When the modulation signal is very slow ($\Omega \ll \Delta \nu _{FSR}/{\mathcal {F}}$), we get the instantaneous frequency of the modulated beam as

$\omega (t)={\frac {d}{dt}}(\omega t+\beta sin\Omega t)=\omega +\Omega \beta cos\Omega t$

Then the reflected power can be written as

$P_{ref}(\omega +\Omega \beta cos\Omega t)\approx P_{ref}(\omega )+{\frac {dP_{ref}}{d\omega }}\Omega \beta cos\Omega t\approx P_{ref}(\omega )+P_{0}{\frac {d|F(\omega )|^{2}}{d\omega }}\Omega \beta cos\Omega t$,

and in this regime, the expression of $F(\omega )F^{*}(\omega +\Omega )-F^{*}(\omega )F(\omega -\Omega )$ is purely real as shown in the following:

$F(\omega )F^{*}(\omega +\Omega )-F^{*}(\omega )F(\omega -\Omega )\approx 2{\mathcal {Re}}[F(\omega ){\frac {d}{d\omega }}F^{*}(\omega )]\Omega \approx {\frac {d|F|^{2}}{d\omega }}\Omega$.

So in the reflection signal, only cosine term survives for the ac signal part. So, we should mix it with a shifted modulation signal, and we will get the error signal as (after the low pass filter)

$\epsilon =P_{0}{\frac {d|F|^{2}}{d\omega }}\Omega \approx 2{\sqrt {P_{c}P_{s}}}{\frac {d|F|^{2}}{d\omega }}\Omega$.

Figure 4 shows the signal with a low frequency modulation.

Figure 4. Error signal with low frequency modulation. From left to right, the figures show the error signal for cavities of fitness equals to $312.58$, $29.80$, and $10.88$ respectively.

Modification to the Project

In this project, instead of locking the laser to a certain frequency, we will lock the cavity length to the laser frequency. By attaching a piezo actuator (PZT) to one end of mirror, we can tune cavity length. Once we align the cavity, making the resonance of it at the laser frequency, from the error signal, we are able to read out the change of the cavity length off the laser frequency, and also lock the cavity to the laser frequency by feed back the error signal to the control system, which will move the PZT to make the cavity resonance at the laser frequency.

In following sections, we introduced how we plan to achieve this goal and what have we done so far.

Experiment Diagram

We plan for a setup.... (the whole setup and explain how we applied the PDH locking)

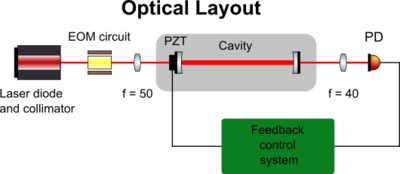
Optical Part

The optical layout for the PDH technique is shown in figure 5. A laser diode is connected with a collimator, which gives the flexibility of adjusting the focal length of the laser. The laser is then sent to the electro-optical modulator (EOM) for adding the 20 MHz sidebands to the incident beam before the cavity. A PZT is attached to the input mirror for scanning the error signal and later locking the cavity length. The focal lens before the cavity is used to adjust the beam width and its position inside the cavity, while the one after is to focus light into the photon detector (PD). The readout signal from PD is sent to the feedback loop circuit for controlling the PZT to lock the cavity length.

Figure 5. Optical layout for the PDH locking.

As shown in figure 2, if we want to have a good locking and read out the cavity length change based on the phase change of the signal, we would have to assume our laser is more stable than the cavity itself, which sets the limit of how good the cavity we can get. In order to estimate the reflectivity of the two mirrors and the length of the cavity, we use the relation of the finesse respect to the reflectivity of the two mirrors, and to the linewidth of the cavity resonance.

${\mathcal {F}}={\frac {\pi {\sqrt {r}}}{1-r}}$,

${\mathcal {F}}={\frac {\kappa }{\Delta \nu _{FSR}}}$,

where $r$ is the reflectivity of the mirrors, and $\kappa$ is the half-linewidth of the cavity resonance. Assuming the laser has a half linewidth less than 10 MHz, we will want a cavity that has a half linewidth of the resonance frequency more than 20 MHz. Thus for a given 10 cm cavity the finesse of the cavity needs to be smaller than 75. Then we decided to use the mirrors that have reflectivity of 95%, which gives us a finesse of 61.24.

Circuit Part

Here we demonstrate the electrical circuits we have used to make an electro optic modulator (EOM) tank circuit and a PDH board that integrates a phase shifter, mixer, amplifier and a PID loop to control and lock the cavity using PDH locking system, as shown in figure 6.

EOM Tank circuit

EOM tank circuit can be simplified down to an LC oscillator circuit whose resonant frequency is the required modulation frequency. The circuit consists of a piezo electric crystal (Lithium Niobate crystal) that changes the polarisation of light passing through it in response to an external electric field (phase modulation). The change in the phase or polarisation of light is due to the change in the refractive index of the crystal. This change can be interpreted as a capacitive effect, where the crystal stores energy in the form of electric field.

Figure 6. EOM tank circuit.

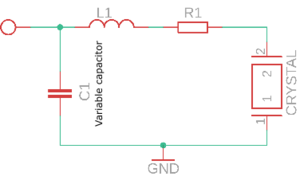
To implement the EOM circuit, the electrodes (conductive metal) are attached to the crystal such that it acts as a variable capacitor, which is then connected to an inductor (L1) and other capacitor (C1) forming an LC circuit as shown in figure 6. The inductor is chosen such that the resonant frequency of the circuit is the required modulation frequency and the dominating capacitance is the capacitance of the crystal.

Here, we require a modulation frequency of 20 MHz, so the resonant frequency of the LC oscillator is 20 MHz and the capacitance of the crystal is 10 pF. Then the required inductance for $\omega ={\frac {1}{\sqrt {LC}}}$ is 6.3 $\mu {\text{H}}$.

The capacitor C1 in the circuit in figure 6 is for obtaining maximum impedance. When the circuit is at resonant frequency and maximum impedance, it leads to highest voltage across the crystal resulting in efficient modulation of light. Also the modulated signal will be transmitted through the crystal with minimum loss. The resonant frequency of the circuit can be inspected using a vector network analyzer (VNA). If there is an impedance mismatch, most of the signal will be reflected back. The inductor L1 can be tuned to obtain the resonant frequency and the capacitor C1 can be varied to obtain maximum impedance for obtaining efficient modulation.

Feedback and Locking Circuit

The circuit board given in figure 7 performs phase shifting, mixing signals, filtering and standard PID control loop for the PDH locking we aim to implement. The input signals to the circuit are: LO input (20 MHz sine signal from function generator), signal input (output from photodetector which is the transmission from the cavity) and the output signals are: control out connecting to the piezo, and the error signal.

To briefly understand the working of the circuit, it can be broken down to parts as shown in figure 7 and explained below:

• Phase shifter: The phase shifter part in the circuit compensates for the delay between the two input signals, LO and signal from detector. Inorder to measure the error signal, we must match the phase of the two signals going into the mixer to produce two pure sine terms at the input of the mixer. This is performed by the phase shifter (JSPHS-26), phase detector (RPD-2) followed by the mixer. The phase shifter works for frequency between 18-26 MHz and a voltage control of 0-12 V for a phase shift between 0-350 degrees. This voltage control is achieved using a BJT amplifier/attenuator circuit.

• Low pass filter: Once we mix down the two signals, the output will contain the sum and difference frequencies. If the two input signals have same frequency, we get a DC or a low frequency signal at the output which can be isolated using a low pass filter. This filtered output is fed to the polarity selector.

• Amplification and polarity control: The filtered output is amplified and send to a polarity selector. The polarity control helps in selecting the phase (positive or negative) of the error signal before sending it to the feedback loop to control the piezo. The error signal is the phase difference between resonant frequency of the new cavity (caused by length change) and the resonant frequency of the reference cavity. The phase of the error signal determines on which side of the cavity resonance we are currently at. The feedback system can then drive the piezo to adjust the cavity length to maintain the resonance condition.

• Voltage biasing: Voltage biasing is applied to the piezoelectric transducer (PZT) to provide a reference position for the cavity length. If the resonant frequency of the cavity sits at some offset voltage, then the PZT needs to be operated around the offset voltage inorder to even obtain an error signal. If the PZT is driven at a voltage far away from the resonant frequency then there would be no error signal. The voltage biasing part of the circuit consists of two variable resistors to set the reference position during the initial alignment of the PDH system. The voltage biasing provides a baseline voltage around which the feedback control system operates, ensuring that adjustments to the PZT voltage are relative to the reference position. This also helps in ensuring linear response of the PZT to the applied voltage.

• PID loop: The voltage applied to the PZT is controlled using the feedback loop that consist of the Proportional (P) part and the Integral (I) part.
  • The output of the proportional part is proportional to the error signal. The P term is responsible for the immediate response of the system to the error signal. To implement this, the circuit is just a proportional amplifier, amplifying the error signal, whose feedback is adjusted using a variable resistor.
  • The integral part integrates the error signal over time. It helps to eliminate steady-state errors and bias in the error signal by continuously adjusting the control signal. It provides long-term stability and ensures that the system reaches and maintains the desired lock point even in the presence of small, persistent errors. The circuit implementation is that of an op-amp integrator.

• Piezo control: The output of the feedback loop is connected to the piezo through an amplifier and to the voltage biasing to set the initial output offset. For the amplifier circuit, the resistor is chosen such that the time constant of the circuit is dominated by the time constant of the PZT as it governs how quickly the cavity is adjusted in response to the voltage. Thus PZT time constant must be dominating to ensure that the system can track and correct frequency deviation efficiently.

The control parameters that are provided are the variable resistors to adjust the voltage biasing, the attenuation of phase shifter and the variable resistors to adjust the feedback of the PID loop.

The output signal is the error signal to be monitored on an oscilloscope.

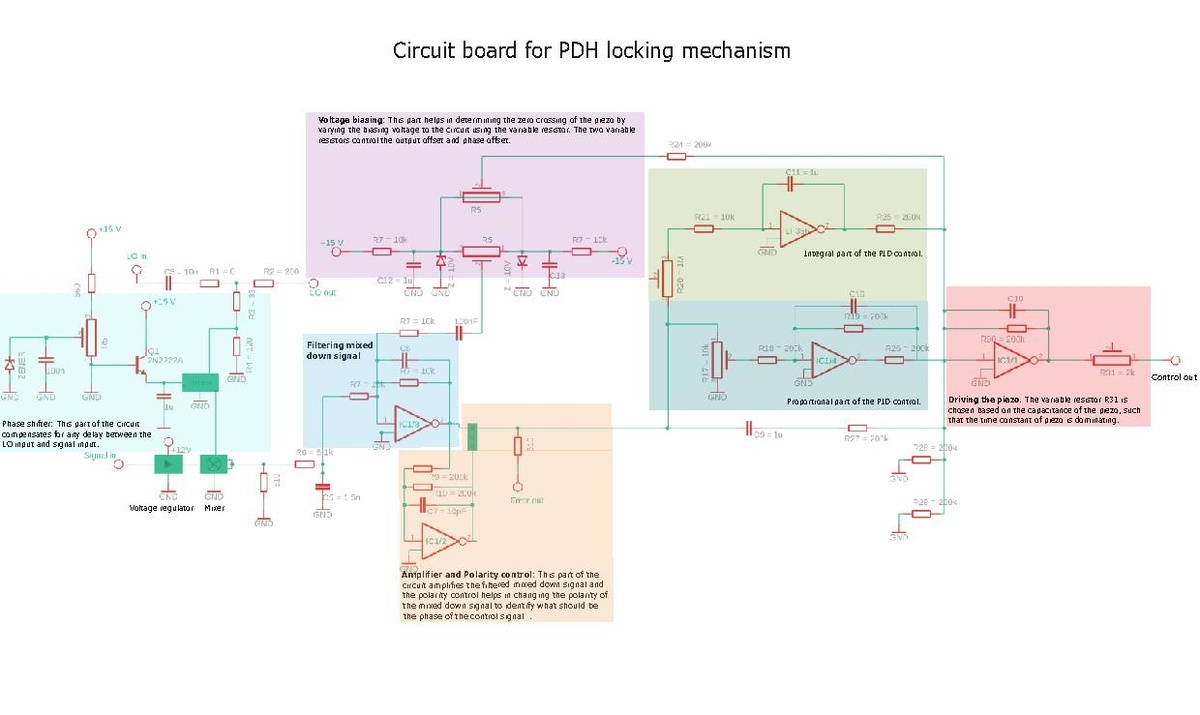
Figure 7. Feedback and Locking circuit.

Setting up the experiment and the measurements

We have made each of the components of this sensor, including the EOM and the control circuit PCB boards, gluing the piezo to the cavity, testing the EOM, and in the end building the setup.

EOM

Figure 8. Home made EOM tank circuit board.

We soldered the EOM tank circuit, which has an inductor, a variable capacitor, and the crystal. Care was taken in soldering the crystal to the circuit board and also while connecting the conductor to the crystal and the board. To solder the crystal to the circuit board, we used low temperature solder paste which liquifies on heating and sucks in creating a tight contact between the crystal and board. In a similar manner, copper sheet is connected to the other side of the crystal and the board as shown in figure 8.

As discussed in the EOM tank circuit part, the resonant frequency of the circuit is determined by the inductance of the inductor and the capacitance of the crystal. As the capacitance of the crystal is fixed, we vary the inductor so that the resonant frequency of the circuit is the required modulation frequency. As shown in figure 9, we used a function generator to sweep a sinusoidal signal from 10 MHz to 30 MHz send to the frequency spectrum analyser (FSA) and the EOM circuit. The reflection signal from the circuit interferes with the one directly sent to FSA.

Figure 9. Measuring the resonant frequency and the scattering of the EOM tank circuit with a frequency spectrum analyser, and finding the proper inductor to generate 20 MHz signal for driving the crystal.

Figure 11. Measuring the resonant frequency and the scattering of the EOM tank circuit with a network analyser, and finding the proper capacitor to send the maximum energy to the crystal.

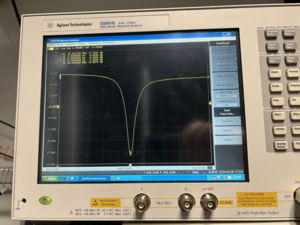
If the signal is fully reflected back from the EOM tank, we infer that the frequency is not the resonant frequency of the circuit, and we see a strong signal (almost all from the function generator) at that frequency. If the scanning frequency is at the resonant frequency of the circuit, only small amount of the power is reflected back, and we see a weak signal at that frequency, which is the dip shown in figure 10. In figure 10, we show how we used FSA to find the resonant frequencies with different inductors, and finally got the correct inductor at 6 uh as calculated above, by connecting a 10 uh and a 15 uh connected in parallel.

Figure 10. Resonant frequency scan for the EOM tank circuit with different inductors. The top figure shows the reference signal without the EOM tank connected to FSA. The rest four figures shows the frequency scan results with the EOM tank connected with different inductors. The scanning frequency is from 10 MHz to 30 MHz, and the resonant frequency increase with the decrease of the inductance of the circuit.

By changing the inductor, we obtain the resonant frequency but may not be having the maximum impedance. For effective modulation, maximum impedance is required which can be obtained by tuning the variable capacitor C1 in such a way that the dominant capacitance of the circuit is still the capacitance of the oscillator. As shown in figure 8, there is a variable capacitor C1 with fine tuning range and provision to add the external capacitors. Figure 12 (left) shows the impedance change of the circuit through fine tuning and the right figure shows a coarse tuning of the impedance by varying the external capacitor along with the variable capacitor of capacitance C.

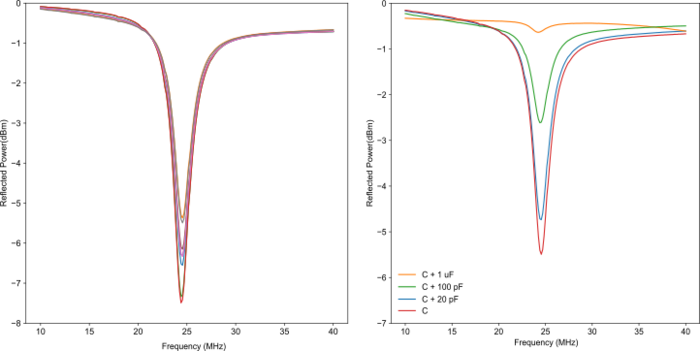
Figure 12. Resonant frequency scan for the EOM tank circuit with different capacitors. Left figure shows the fine tuning of the impedance by varying the variable oscillator. Right figure is a more coarse tuning by adding external capacitors.

Feedback and locking circuit

Figure 13. The home-made feedback control circuit.

Figure 13 shows the feedback control circuit we have made. It is the circuit shown in figure 7. Care was taken while soldering some of the parts in the board, especially the phase shifter and chip resistors. Inorder to keep the cross-talk between different segments as low as possible the components are surrounded by lot of ground plane. This makes it difficult to solder. So the PCB board was initially heated to about 200$^{\circ }$C while soldering.

Cavity

We attached a piezo on one end of mirror in the cavity, as shown in figure

Figure 14. The cavity with a piezo attached in between.

Test setup

Figure 15. Schematic representation of the test setup for PDH locking of the cavity

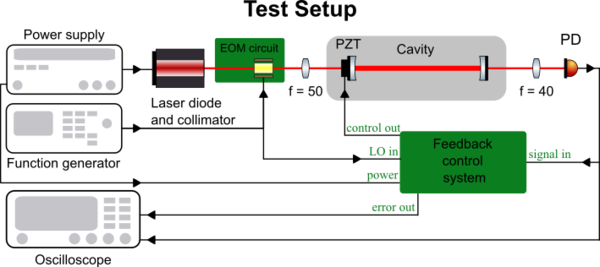
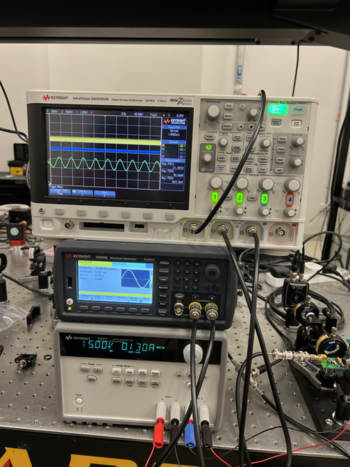
Figure 15 shows our test setup consisting of the home made EOM, cavity and home made feedback circuit to implement PDH locking to lock the cavity to the laser. As shown in figure, Power supply is used to drive the laser diode, operating at 2V and to give a constant voltage of 15 V to the feedback circuit board. A sinusoidal signal at 20 MHz and amplitude of 5Vpp is generated used a function generated and sent to both EOM tank circuit and as LO to the feedback circuit board. The laser is first aligned to the EOM crystal, which then reaches the cavity and the transmission from the cavity is detected using a photodetector. The photodetector output is then fed to the feedback circuit as signal in and it is also monitored on the oscilloscope. The output from feedback circuit, which is the error signal is monitored using an oscilloscope. So in our setup, we monitor three signals, the LO signal from function generator, transmission signal from the cavity and the error signal from the feedback circuit.

Test the modulation part

Figure 16. Testing the modulation produced by EOM tank circuit for various modulation depth

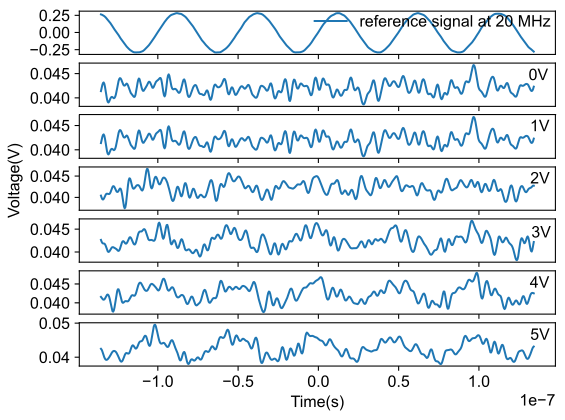
We first tested the EOM tank circuit, to check if the board could produce any modulation at all. The test setup is similar as shown in figure 15, but the photodetector is now placed right after the EOM tank circuit, to check the modulated light using an oscilloscope. The results are shown in figure 16. We see that our EOM does produce modulate the signal. For a modulation depth of 5V, we could see the modulation clearly.

Test the control part

Figure 17. Experimental setup for sensing the displacement of the mirrors via PDH technique.

Discussion and Conclusion

In this project, we have learnt a lot of things, and finished most of the preparation work. We soldered the circuits, found the correct inductance and the capacitance for the EOM tank, we saw the modulation of the EOM, setup the experiments. However, to achieve locking, to implement the circuit and the PDH locking in this setup, there are still some steps to do.

• We will need to scan the piezo without the laser being modulated, and align the cavity, that will need us to separate the two mirrors so that we can adjust the distance and the tilting of the mirrors. We will also need two mirrors outside the cavity to walk the beam.
• After aligning the cavity, we will then turn on the EOM tank circuit, adding modulation to the input laser, and try to see the error signal.
• Then, based on the scanning of error signal, we need to find the offset of the piezo driving voltage that allows the piezo to stay near the resonance of the cavity.
• Around that offset, we use the control circuit to lock the cavity.
• Once the control loop works, we are able to readout the distance change of the cavity length with the error signal.

Reference

• Black, E. D. (2001). An introduction to Pound–Drever–Hall laser frequency stabilization. American journal of physics, 69(1), 79-87.