Gas sensor
Introduction
The semiconductor gas sensor for carbon monoxide/combustible gas detection uses a gas-sensitive material, tin dioxide (SnO2), which has a low conductivity in clean air. The high and low-temperature cycle detection method is used to detect carbon monoxide at low temperature (1.5V heating), where the conductivity of the sensor increases with the concentration of carbon monoxide gas in the air, and to detect the combustible gases methane and propane at high temperature (5.0V heating), and to clean up the stray gases that are adsorbed at low temperature. A simple circuit is used to convert the change in conductivity to an output signal corresponding to the concentration of the gas.
Team Members
Fu Xinming, Ge Yexiao, Yang Haoqing
Setup
The diagram above shows the basic test circuit for the sensor. The sensor requires two voltages to be applied: the heater voltage (VH) and the test voltage (VC). VH is used to provide the sensor with a specific operating temperature and VC is used to determine the voltage (VRL) across the load resistor (RL) connected in series with the sensor. VC is used to determine the voltage (VRL) across the load resistor (RL) in series with the sensor. The sensor has a slight VC requires a DC power supply. VC and VH can be used as long as the electrical requirements of the sensor are met. VC and VH can share the same power supply circuit if the electrical requirements of the sensor are met. To take advantage of the sensor's performance of the sensor, it is necessary to select the appropriate RL value.
Equipment
Gas Sensitive Components
One-chip computer/microcontroller
ADC conversion module
Gas Sensor Datasheet
Timeline and Milestone
| Week 8 (3/4 — 3/8) | Debug sensor module hardware devices and software code | |
| Week 9 — Week 10(3/11 — 3/22) | Measurements using gas sensors to obtain a database | |
| Week 11 — Week 12(3/25 — 4/5) | Fit curve to obtain the corresponding relationship between the output value and the gas concentration | |
| Week 13 (4/8 — 4/12) | Analyze experimental results and complete reports |
Expected Results
We hope to obtain a curve between the output value and the corresponding gas concentration, so as to know the pollution situation in the environment relatively accurately.
Report
Introduction
Band Theory
Band theory explains that within a crystal lattice, there exists a valence band and a conduction band separated by an energy gap, which is closely related to the Fermi level. The Fermi level is defined as the highest energy level occupied by electrons at absolute zero temperature. Based on the size of the energy gap between these bands, materials are classified into three main categories:

Insulators: These materials have a substantial gap between the valence and conduction bands, typically around 10 eV or more. Due to this large gap, a significant amount of energy is needed to move an electron into the conduction band, resulting in negligible electronic conduction. At zero temperature, the Fermi level represents the highest filled state.
Semiconductors: These materials feature an energy gap ranging from about 0.5 to 5.0 eV. Below the Fermi level, electrons do not have enough energy to bridge this gap, preventing conduction. However, once the energy exceeds the Fermi level, electrons can transition to the conduction band, leading to increased electrical conductivity.
Conductors: In conductors, the Fermi level is positioned within the conduction band itself, allowing for continuous electron flow and high conductivity.
Band Theory in Gas Sensors
Band theory has played a crucial role in understanding the functionality of gas sensors for several years. In this context, the interaction between a target gas and a metal oxide film's surface—typically involving surface adsorbed oxygen ions—causes a shift in the material's charge carrier concentration. This shift subsequently affects the material's conductivity or resistivity.
For n-type materials, oxidizing gases increase the resistance of the thin film, while reducing gases decrease it. The opposite is true for p-type materials. This interaction, involving oxidation-reduction (REDOX) reactions, alongside the transduction function, defines the chemiresistive behavior of these sensors. Metal oxide sensors are commonly configured as sintered pellets or as thick and thin films. The specific geometry of the crystallites and their interconnections significantly influence these receptor and transduction functions, highlighting the impact of nanotechnology in enhancing sensor performance by manipulating materials at the atomic and molecular scale.
On the other hand, p-type semiconductors, where positive holes are the majority charge carriers, exhibit increased conductivity in the presence of an oxidizing gas, which augments the number of positive holes. Conversely, the presence of a reducing gas increases the material's resistance by introducing negative charge that diminishes the concentration of positive charge carriers (holes). The various responses of these materials to different gases are summarized in Table 1.
| Classification | Oxidising Gases | Reducing Gases |
|---|---|---|
| n-type | Resistance increase | Resistance decrease |
| p-type | Resistance decrease | Resistance increase |
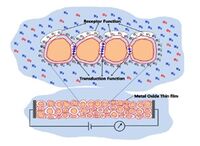
The chemiresistance of metal oxides is also linked to the width of the space charge region that forms on the crystallites due to electron transfer during the adsorption and desorption of gas molecules. This space charge region creates a potential barrier that affects conduction between the grains, leading to changes in the Fermi level. In n-type materials, the interaction with oxidizing gases causes the energy bands to bend upward as electrons are depleted, whereas with reducing gases, the bands bend downward due to electron accumulation. Thus, the space charge region and band bending are closely related to the carrier concentrations within the grain, which are influenced by the grain's size and shape.