Laser Distance Measurer: Difference between revisions
| (17 intermediate revisions by 2 users not shown) | |||
| Line 30: | Line 30: | ||
# Function generator that can output square wave signal (model used: Tektronix AFG1022) | # Function generator that can output square wave signal (model used: Tektronix AFG1022) | ||
# DC power supply for photodetector (model used: Keithley 2231A-30-3) | # DC power supply for photodetector (model used: Keithley 2231A-30-3) | ||
# Hamamatsu S5971 silicon | # Hamamatsu S5971 silicon photodetectorwith an amplifier | ||
# 650 nm (red) LED | # 650 nm (red) LED | ||
# Aspheric lens (model used: Thorlabs F220FC-B, f = 10.99 mm) | # Aspheric lens (model used: Thorlabs F220FC-B, f = 10.99 mm) | ||
# Mirror | # Mirror | ||
# | # Linear translation stage | ||
# Optical breadboard, postholders and screws | # Optical breadboard, postholders and screws | ||
# Ruler or measuring tape | # Ruler or measuring tape | ||
# BNC cables | # BNC cables | ||
== | ==Experiment Setup== | ||
For a visual of the completed setup, please refer to figure 5 and the accopmanying circuit diagram. | |||
====Laser Modulation and System Initialisation==== | ====Laser Modulation and System Initialisation==== | ||
Configure the function generator to output a 10 MHz square wave with an amplitude of | Configure the function generator to output a 10 MHz square wave with an amplitude of 1 to 3.1 V (High level: 3.1 V, Low level: 1.0 V, output impedance: 50 Ω) to modulate the laser diode. Connect the function generator to the oscilloscope and verify that the signal output from the function generator can be observed on the oscilloscope. Use a T-section to connect the oscilloscope (same port used by the function generator) to the laser LED, and verify that (when the function output is on) visible light is emitted from the laser. Connect the DC power supply set to constant voltage (5.0 V in this setup) to the photodiode. | ||
====Optical Alignment==== | ====Optical Alignment==== | ||
Mount the 650 nm laser diode and use the aspheric lens to collimate and focus the beam onto the reflective target surface. The lens should be placed in a cage plate and mounted in a position such that the distance between the lens and the LED is the focal length of the lens. | Mount the 650 nm laser diode on the linear translation stage and use the aspheric lens to collimate and focus the beam onto the reflective target surface. The lens should be placed in a cage plate and mounted in a position such that the distance between the lens and the LED is the focal length of the lens. (Note: the LED--and the detector below--should be mounted on the translation stage via postholders so that their heights are adjustable.) | ||
{| style="border:none; margin:auto; text-align:center;" | {| style="border:none; margin:auto; text-align:center;" | ||
| Line 58: | Line 58: | ||
====Detection and Amplification Circuit Configuration==== | ====Detection and Amplification Circuit Configuration==== | ||
For the photodetector, | For the photodetector, mount the Hamamatsu S5971 silicon photodiode to a position on the translation stage such that it can detect the light signal. To amplify the signal linearly without saturation, the detector output is connected to a high-speed preamplifier (bandwidth >100 MHz, gain ∼10³–10⁵). Connect the detector/amplifier combination to Channel 2 of a digital oscilloscope; compare it to the reference signal from the function generator (Channel 1) as the modulation phase reference; the two signals should be out of phase. | ||
{| style="border:none; margin:auto; text-align:center;" | {| style="border:none; margin:auto; text-align:center;" | ||
| Line 67: | Line 67: | ||
|} | |} | ||
====Recording the Time Delay vs. Distance Mapping==== | |||
Turn on the LED and ensure that the beam is collimated by adjusting the distance of the lens to the LED. With the light from LED hitting the photodetector, observe the function generated on the oscilloscope. Use the oscilloscope’s cursor measurement function to determine the relative time delay Δt between the modulation reference signal (Channel 1) and the return signal (Channel 2). Correlate the measured delay values with corresponding distances to establish the system’s delay–distance response curve. | |||
With the apparatus in place, the following procedure outlines how to measure the time delay and the corresponding distance: | |||
# Use a meter ruler to mark the distance along the translation stage. | # Use a meter ruler to mark the distance along the translation stage. | ||
# Move the LED source to the marked positions (e.g. 30 cm from detector) and adjust the beam until it is centralised on the photodetector. | # Move the LED source to the marked positions (e.g. 30 cm from detector) and adjust the beam until it is centralised on the photodetector. | ||
# Measure the time delay on the oscilloscope. Record the minimum, maximum and mean time delay—take three readings per distance and average them. | # Measure the time delay on the oscilloscope. Record the minimum, maximum and mean time delay—take three readings per distance and average them. | ||
# '''Repeat steps | # '''Repeat steps 1–3 for different distances''' on the translation stage. | ||
# Insert a mirror in the setup to act as the “object we are trying to measure the distance of”, so that the beam path is reflected off the mirror to the photodetector. | # Insert a mirror in the setup to act as the “object we are trying to measure the distance of”, so that the beam path is reflected off the mirror to the photodetector. | ||
# Measure the total path length manually and '''repeat steps | # Measure the total path length manually and '''repeat steps 1–3''' for each mirror position. | ||
| Line 97: | Line 99: | ||
==Results== | ==Results== | ||
{| style="border:none; margin:auto; text-align:center;" | {| style="border:none; margin:auto; text-align:center;" | ||
|- | |- | ||
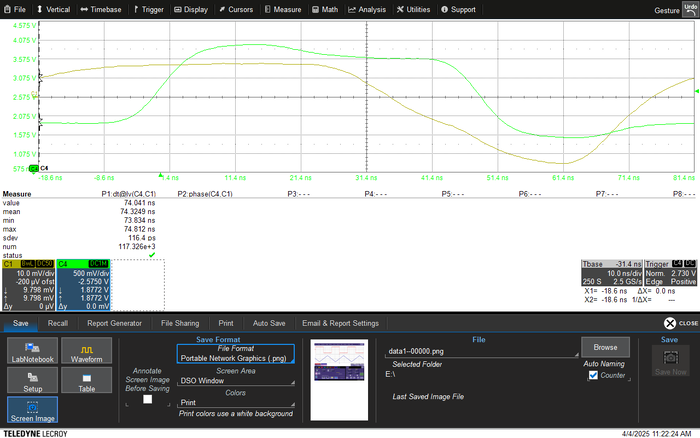
| [[File:reference.png|700px]] | | [[File:reference.png|700px]] | ||
|- | |||
| '''Figure 6.''' Delay between the function generator and the received signal by the photodetector on the oscilloscope. Green graph represents the function generated by the function generator and the yellow graph represents the function produced from received the laser beam by the detector. | |||
|} | |} | ||
| Line 113: | Line 116: | ||
|} | |} | ||
The measured delay time is in the order of 20-30 | The measured delay time is in the order of 20-30 ns, which, when calculated, gives about 6-9 m of distance. However, our incremental changes in the distance between the LED and the photodetector were in the order of 10-80 cm. Hence, it was evident that this additional delay time was occurring due to all the cables attached to the oscilloscope and function generation and the distance between the laser and the detector. The length of the BNC cables was 410 cm. This would lead to an additional delay of 13.7 ns. We hypothesise that the rest of the delay is due to the internal wiring functions of the oscilloscope. | ||
| Line 123: | Line 126: | ||
| [[File:data2.png|600px]] | | [[File:data2.png|600px]] | ||
|- | |- | ||
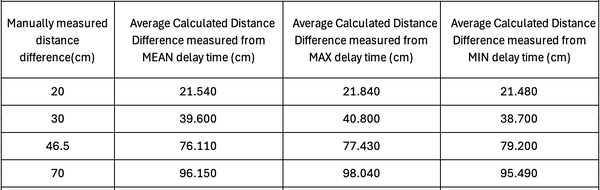
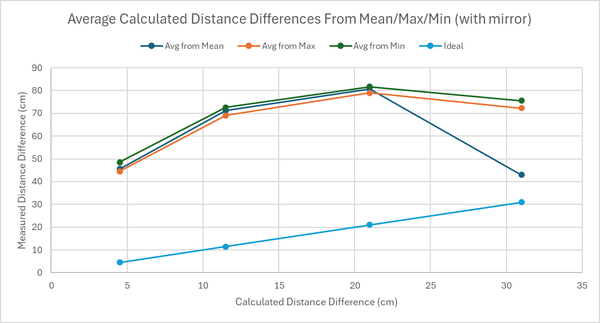
| '''Table 3.''' Calculated Average Distance Difference from delay time vs Manually measured distance between LED and photodetector. Separation distance of ''' | | '''Table 3.''' Calculated Average Distance Difference from delay time vs Manually measured distance between LED and photodetector. Separation distance of '''10 cm''' was taken as the "reference" distance and the successive distances were subtracted from it to give "absolute" values. | ||
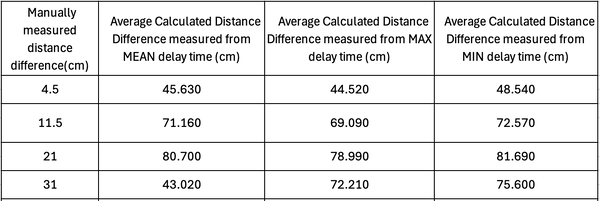
| '''Table 4.''' Calculated Average Distance Difference from delay time vs Manually measured distance between LED and photodetector with the mirror acting as the "object". Separation distance of '''46. | | '''Table 4.''' Calculated Average Distance Difference from delay time vs Manually measured distance between LED and photodetector with the mirror acting as the "object". Separation distance of '''46.5 cm'''was taken as the "reference" distance and the successive distances were subtracted from it to give "absolute" values. | ||
|} | |} | ||
| Line 136: | Line 139: | ||
|} | |} | ||
We can calculate the uncertainty using the standard error which is <math>\frac{\sigma}{\sqrt{n}}</math> where <math>\sigma</math> is the standard deviation of the raw data and n is the number of samples. This will be the <math>\delta t_i</math>. | |||
<math>\delta d = d \times \sqrt{\bigl(\frac{\delta t}{t_1 - t_2}\bigr)^2}</math> | Then to calculate uncertainty for difference in delay: <math>\delta t = \sqrt{(\delta t_1)^2 + (\delta t_2)^2}</math> | ||
Finally, the uncertainty of calculated difference distance from delay time: <math>\delta d = d \times \sqrt{\bigl(\frac{\delta t}{t_1 - t_2}\bigr)^2}</math> | |||
| Line 146: | Line 151: | ||
| [[File:final2.png|600px]] | | [[File:final2.png|600px]] | ||
|- | |- | ||
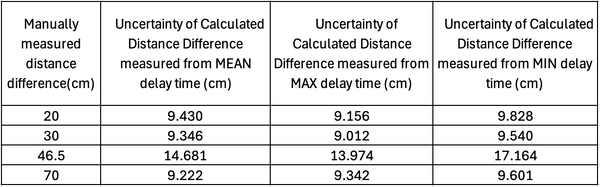
| '''Table 5.''' | | '''Table 5.''' Uncertainty of Distance Difference from delay time without mirror. | ||
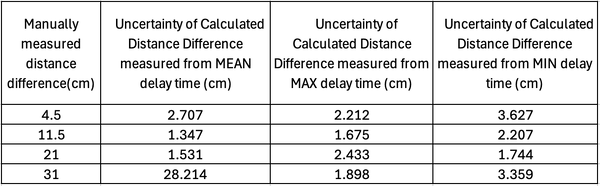
| '''Table 6.''' | | '''Table 6.''' Uncertainty of Distance Difference from delay time with a mirror acting as the "object" | ||
|} | |} | ||
| Line 163: | Line 168: | ||
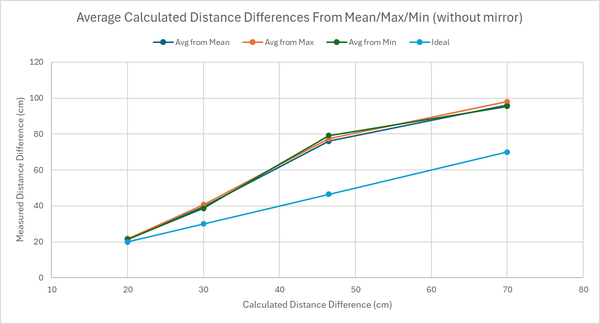
Though the project's concept was fairly straightforward, the yielded results were not precise within the instruments' uncertainty. The uncertainty of the meter ruler was <math>\pm 0.1cm</math> and the uncertainty of the oscilloscope was <math>\pm 0.001ns</math>. | Though the project's concept was fairly straightforward, the yielded results were not precise within the instruments' uncertainty. The uncertainty of the meter ruler was <math>\pm 0.1cm</math> and the uncertainty of the oscilloscope was <math>\pm 0.001ns</math>. Furthermore, the values obtained go beyond the calculated uncertainties in Table 5 and 6. This shows that the main source of error was experimental, likely due to the challenges mentioned such as the lack of a focusing mirror, which caused fluctuations in the delay. The data obtained from calculating the distance difference is ~20-30cm higher than the manually measured distance, which makes it quite inaccurate. To reduce the inaccuracies, the measured distance difference can be larger, in the order of meters. This would mean that the changes in the delay would be in the order of a few nanoseconds rather than a few tenths of a nanosecond, reducing the error from the fluctuation. However, aligning the LED onto the detector would be even more difficult and might cause more fluctuations on the delay if there is no focusing lens. | ||
==Improvements and Future Work== | ==Improvements and Future Work== | ||
Latest revision as of 19:55, 29 April 2025
Group Members
Arya Chowdhury, Liu Sijin, Jonathan Wong
Background and Theory
Laser-based distance measurement is a technique to measure distances remotely when on-site measurement becomes inconvenient. This has many applications such as autonomous driving, radar, and precision manufacturing. The working principle of using lasers to measure such distances can generally be categorised into one of three approaches: pulsed time-of-flight (ToF), optical triangulation and phase-shift continuous-wave (CW) measurement[1]. Here we will construct an apparatus according to the third approach.
Mathematical Background on Phase-Shift Distance Measurement
When a CW laser is intensity-modulated at frequency , round-trip propagation to a target introduces a phase delay
,
where d is the one-way distance and c is the speed of light[2]. Solving for d gives
Because phase is measured modulo , the maximum unambiguous range is
[3]
For , , adequate for laboratory-scale demonstrations.
For our experiment, using an oscilloscope, you can measure the phase delay between generated wave and reflected wave. This makes the task of finding the distance based on phase delay much simpler. where c is the speed of light.
Equipment List
- Oscilloscope
- Function generator that can output square wave signal (model used: Tektronix AFG1022)
- DC power supply for photodetector (model used: Keithley 2231A-30-3)
- Hamamatsu S5971 silicon photodetectorwith an amplifier
- 650 nm (red) LED
- Aspheric lens (model used: Thorlabs F220FC-B, f = 10.99 mm)
- Mirror
- Linear translation stage
- Optical breadboard, postholders and screws
- Ruler or measuring tape
- BNC cables
Experiment Setup
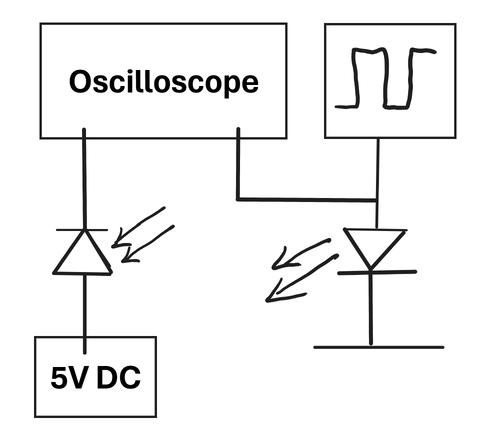
For a visual of the completed setup, please refer to figure 5 and the accopmanying circuit diagram.
Laser Modulation and System Initialisation
Configure the function generator to output a 10 MHz square wave with an amplitude of 1 to 3.1 V (High level: 3.1 V, Low level: 1.0 V, output impedance: 50 Ω) to modulate the laser diode. Connect the function generator to the oscilloscope and verify that the signal output from the function generator can be observed on the oscilloscope. Use a T-section to connect the oscilloscope (same port used by the function generator) to the laser LED, and verify that (when the function output is on) visible light is emitted from the laser. Connect the DC power supply set to constant voltage (5.0 V in this setup) to the photodiode.
Optical Alignment
Mount the 650 nm laser diode on the linear translation stage and use the aspheric lens to collimate and focus the beam onto the reflective target surface. The lens should be placed in a cage plate and mounted in a position such that the distance between the lens and the LED is the focal length of the lens. (Note: the LED--and the detector below--should be mounted on the translation stage via postholders so that their heights are adjustable.)

|

|
| Figure 1. Front view of collimating lens for laser diode | Figure 2. Side view of collimating lens for laser diode |
Detection and Amplification Circuit Configuration
For the photodetector, mount the Hamamatsu S5971 silicon photodiode to a position on the translation stage such that it can detect the light signal. To amplify the signal linearly without saturation, the detector output is connected to a high-speed preamplifier (bandwidth >100 MHz, gain ∼10³–10⁵). Connect the detector/amplifier combination to Channel 2 of a digital oscilloscope; compare it to the reference signal from the function generator (Channel 1) as the modulation phase reference; the two signals should be out of phase.

|
| Figure 3. Hamamatsu S5971 silicon photodiode with amplifier |
Recording the Time Delay vs. Distance Mapping
Turn on the LED and ensure that the beam is collimated by adjusting the distance of the lens to the LED. With the light from LED hitting the photodetector, observe the function generated on the oscilloscope. Use the oscilloscope’s cursor measurement function to determine the relative time delay Δt between the modulation reference signal (Channel 1) and the return signal (Channel 2). Correlate the measured delay values with corresponding distances to establish the system’s delay–distance response curve.
With the apparatus in place, the following procedure outlines how to measure the time delay and the corresponding distance:
- Use a meter ruler to mark the distance along the translation stage.
- Move the LED source to the marked positions (e.g. 30 cm from detector) and adjust the beam until it is centralised on the photodetector.
- Measure the time delay on the oscilloscope. Record the minimum, maximum and mean time delay—take three readings per distance and average them.
- Repeat steps 1–3 for different distances on the translation stage.
- Insert a mirror in the setup to act as the “object we are trying to measure the distance of”, so that the beam path is reflected off the mirror to the photodetector.
- Measure the total path length manually and repeat steps 1–3 for each mirror position.

|
| Figure 4. Measurement experimental setup without mirror: LED and photodetector on translation stage. |

|
| Figure 5. Measurement experimental setup with mirror acting as the “object.” |
Results
|
|
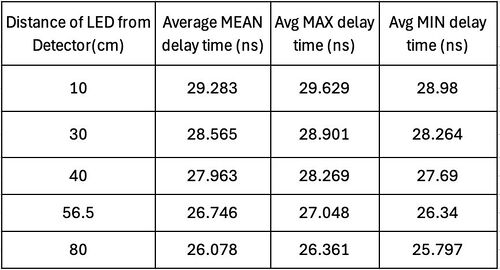
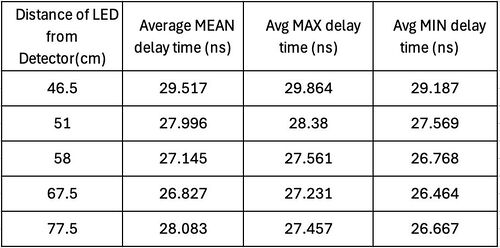
| Table 1. Measured delay time vs manually measured distance between LED and photodetector | Table 2. Measured delay time vs manually measured distance with mirror acting as the “object.” |
The measured delay time is in the order of 20-30 ns, which, when calculated, gives about 6-9 m of distance. However, our incremental changes in the distance between the LED and the photodetector were in the order of 10-80 cm. Hence, it was evident that this additional delay time was occurring due to all the cables attached to the oscilloscope and function generation and the distance between the laser and the detector. The length of the BNC cables was 410 cm. This would lead to an additional delay of 13.7 ns. We hypothesise that the rest of the delay is due to the internal wiring functions of the oscilloscope.
To account for this, we took the shortest distance as our reference distance. The difference between the successive measured distances and the shortest distance gives us the "absolute" distance. We can refer to this as distance difference. We can do this for the measured delay time as well. Take the delay time for the shortest manually measured distance and subtract it from the successive delay times to get an absolute delay time. Another method we thought of was simply plotting a linear plot of manually measured distance vs the delay time and obtaining the y-intercept, which would be the additional delay time due to the system and the cables. One could then subtract this additional delay time from the system from each measured delay time. However, when we measured the gradient of this linear plot on multiple days, the gradient was slightly different each time the measurements were carried out. Hence, we decided to adopt the former approach.
We can calculate the uncertainty using the standard error which is where is the standard deviation of the raw data and n is the number of samples. This will be the .
Then to calculate uncertainty for difference in delay:
Finally, the uncertainty of calculated difference distance from delay time:
|
|
| Table 5. Uncertainty of Distance Difference from delay time without mirror. | Table 6. Uncertainty of Distance Difference from delay time with a mirror acting as the "object" |
Challenges and Conclusion
- One of the challenges we faced was centring the beam onto the photodetector. Due to the lack of a focusing beam on the photodetector, the laser beam spot size was much larger than the surface area of the photodetector. What this led to was a constant fluctuation of the delay time on the oscilloscope as the brightest part of the beam was not always centred on the photodetector despite optimising stabilisation of the beam path. The beam spot on the detector is shown in Figure 9.
- To have accurate distance measurements in the centimetre regime, the delay time we required was ~0.3ns for every 10cm. However, the fluctuation of the delay time on the oscilloscope was causing the 1st decimal place to fluctuate constantly.
- There might have also been a possibility of saturating our photodetector, as our beam was incident directly on it. We tried to reduce the input voltage to the LED, but reducing the voltage below 3V led to no signal appearing on the oscilloscope.

|
| Figure 9. Beam spot on photodetector |
Though the project's concept was fairly straightforward, the yielded results were not precise within the instruments' uncertainty. The uncertainty of the meter ruler was and the uncertainty of the oscilloscope was . Furthermore, the values obtained go beyond the calculated uncertainties in Table 5 and 6. This shows that the main source of error was experimental, likely due to the challenges mentioned such as the lack of a focusing mirror, which caused fluctuations in the delay. The data obtained from calculating the distance difference is ~20-30cm higher than the manually measured distance, which makes it quite inaccurate. To reduce the inaccuracies, the measured distance difference can be larger, in the order of meters. This would mean that the changes in the delay would be in the order of a few nanoseconds rather than a few tenths of a nanosecond, reducing the error from the fluctuation. However, aligning the LED onto the detector would be even more difficult and might cause more fluctuations on the delay if there is no focusing lens.
Improvements and Future Work
- Install a focusing lens for the photodetector to reduce the fluctuation of the time delay on the oscilloscope.
- Use a bandpass filter at 650 nm laser to filter out other frequencies to get less fluctuations in the delay time reading on the oscilloscope.
- Longer translating stage for longer distance measurement
References
[1] Blais, F. (2004). Review of 20 Years of Range Sensor Development. Journal of Laser Applications, 17(4), 208–220. [1]
[2] Wu, D. (2022). Phase-Shift Laser Ranging Technology Based on Multi-Frequency Modulation. Photonics, 9(9), 603. [2]
[3] Li, Y. (2023). Phase-Modulated Continuous-Wave Coherent Ranging Method for High-Precision Measurement. Optics Express, 31(4), 6514–6524. [3]