Ultrasonic Doppler Speedometer: Difference between revisions
| Line 49: | Line 49: | ||
===Digital Filtering=== | ===Digital Filtering=== | ||
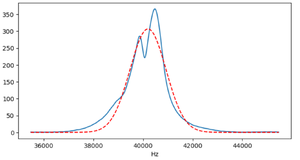
To remove the background noise, we apply a digital filter. After filtering, the frequency spectrum and waveform are significantly improved, showing much less noise (mean frequency | To remove the background noise, we apply a digital filter. After filtering, the frequency spectrum and waveform are significantly improved, showing much less noise. We also fit the filtered frequency spectrum using a Gaussian (normal distribution) curve to estimate the dominant frequency component, which results in a mean frequency of 40012.77 Hz. The filtered results are shown below: | ||
[[File:FilteredSpectrum.png|300px|Filtered frequency spectrum (mean frequency = 40012.77 Hz)]] | [[File:FilteredSpectrum.png|300px|Filtered frequency spectrum with Gaussian fit (mean frequency = 40012.77 Hz)]] | ||
[[File:FilteredWaveform.png|300px|Filtered waveform after noise reduction]] | [[File:FilteredWaveform.png|300px|Filtered waveform after noise reduction]] | ||
Revision as of 22:49, 22 April 2025
Objective
(1) Understand the principles of the ultrasonic Doppler effect and its application in speed measurement.
(2) Design and build an ultrasonic Doppler speedometer to measure the velocity of a moving object.
(3) Analyze experimental data and improve measurement accuracy.
Principle
The ultrasonic Doppler effect states that when ultrasonic waves encounter a moving target (such as a small car or fluid), the frequency of the reflected wave shifts. The frequency shift Δf is related to the velocity v of the target as follows:
where c is the speed of sound in air; θ is the angle between the wave propagation direction and the target's motion.
Experimental Instruments and Setup
Introduction to Experimental Apparatus and Principles
Experimental Setup
Methods and Results
Raw Data
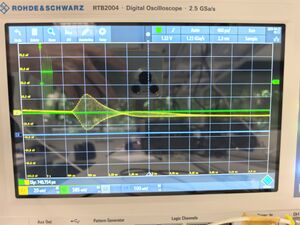
First, we display the waveform shown on the oscilloscope. The following image shows the transmitted and received waveforms.
Waveform Analysis and Fourier Transform
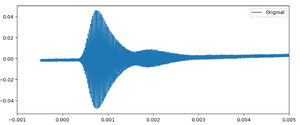
Next, we analyze the waveforms using Python. The transmitted waveform is a square wave, while the received waveform is more complex, resembling a sinusoidal waveform that is a sum of many sine waves.
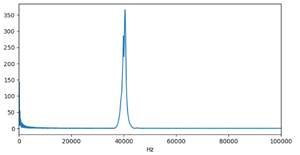
We perform a Fourier Transform on the received waveform to analyze its frequency content. The Fourier transform result is as follows:
From this plot, we observe that the received waveform contains a significant amount of low-frequency noise, which we need to filter out.
Digital Filtering
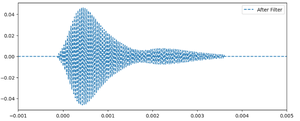
To remove the background noise, we apply a digital filter. After filtering, the frequency spectrum and waveform are significantly improved, showing much less noise. We also fit the filtered frequency spectrum using a Gaussian (normal distribution) curve to estimate the dominant frequency component, which results in a mean frequency of 40012.77 Hz. The filtered results are shown below:
As shown, the noise is greatly reduced after filtering, making the waveform more suitable for experimental analysis.
Measurement of Sound Velocity
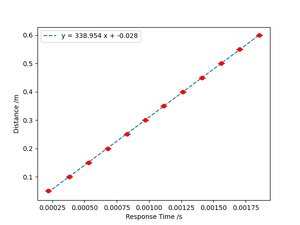
We measured waveforms from the detected sensor with various sensor-sensor distances. Considering the time difference between the transmitting sensor's waveform and the detecting sensor's waveform as the response time that the ultrasonic wave spreads this distance, we plotted the response time versus distance curve as follows,
In this plot, we can find the slope in the fitted curve around 338.95 m/s, which is close to the air sound velocity (343 m/s) with an error of around 1.18%.