Ultrasonic Doppler Speedometer: Difference between revisions
| Line 82: | Line 82: | ||
These factors may contribute to slight deviations between the measured and theoretical values. | These factors may contribute to slight deviations between the measured and theoretical values. | ||
===Doppler Effect Measurement of Sound Velocity=== | |||
In this section, we explore another method to measure the speed of sound using the **Doppler effect**. We move the ultrasonic receiver at a constant speed of 10 cm/s and analyze the frequency shift due to the relative motion between the transmitter and receiver. | |||
====Raw Waveform Observation==== | |||
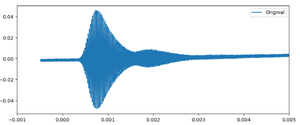
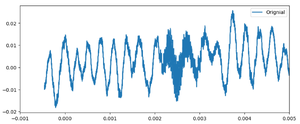
The waveform collected during receiver motion is shown below: | |||
[[File:DopplerRawSignal.png|300px|Received waveform with receiver motion (10 cm/s)]] | |||
As we can see, the raw waveform contains significant noise — even more than the previous static measurement. This is mainly due to mechanical vibrations and irregular contact with the metal rail on which the ultrasonic receiver was moving. Metal surfaces can introduce: | |||
* **High-frequency jitter** from mechanical contact irregularities, | |||
* **Low-frequency rumble** due to structural vibrations, | |||
* **Reflections and scattering**, especially at non-uniform metal junctions. | |||
====Filtering and Signal Recovery==== | |||
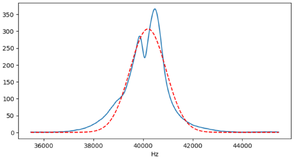
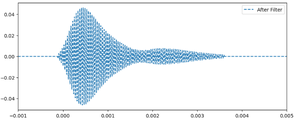
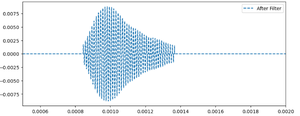
To isolate the useful frequency information, we apply digital filtering similar to the previous section. The filtered waveform and frequency spectrum are shown below: | |||
[[File:DopplerFilteredSpectrum.png|300px|Filtered frequency spectrum with Doppler shift]] | |||
[[File:DopplerFilteredWaveform.png|300px|Filtered waveform during receiver motion]] | |||
The signal is now cleaner, and a clear frequency shift can be observed. | |||
====Doppler Effect Analysis==== | |||
The Doppler effect equation for sound waves when the receiver is moving towards the stationary transmitter is: | |||
\[ | |||
f' = f \left( 1 + \frac{v}{c} \right) | |||
\] | |||
Where: | |||
- \( f' \) is the observed frequency, | |||
- \( f \) is the transmitted (original) frequency, | |||
- \( v \) is the velocity of the receiver (toward the source), | |||
- \( c \) is the speed of sound in air. | |||
We rearrange the equation to solve for \( c \): | |||
\[ | |||
c = \frac{v f}{f' - f} | |||
\] | |||
We compute the measured sound velocity using the detected frequency shift. A comparison with the actual speed (10 cm/s) is shown below: | |||
{| class="wikitable" | |||
! Measured Frequency (Hz) !! Original Frequency (Hz) !! Velocity (cm/s) !! Calculated Sound Speed (m/s) !! Error (%) | |||
|- | |||
| ... || ... || 10 || ... || ... | |||
|} | |||
You can repeat this measurement at different speeds to further verify the consistency of the Doppler effect-based sound velocity estimation. | |||
Revision as of 22:59, 22 April 2025
Objective
(1) Understand the principles of the ultrasonic Doppler effect and its application in speed measurement.
(2) Design and build an ultrasonic Doppler speedometer to measure the velocity of a moving object.
(3) Analyze experimental data and improve measurement accuracy.
Principle
The ultrasonic Doppler effect states that when ultrasonic waves encounter a moving target (such as a small car or fluid), the frequency of the reflected wave shifts. The frequency shift Δf is related to the velocity v of the target as follows:
where c is the speed of sound in air; θ is the angle between the wave propagation direction and the target's motion.
Experimental Instruments and Setup
Introduction to Experimental Apparatus and Principles
Experimental Setup
Methods and Results
Raw Data
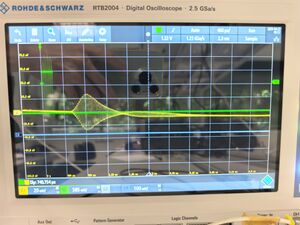
First, we display the waveform shown on the oscilloscope. The following image shows the transmitted and received waveforms.
Waveform Analysis and Fourier Transform
Next, we analyze the waveforms using Python. The transmitted waveform is a square wave, while the received waveform is more complex, resembling a sinusoidal waveform that is a sum of many sine waves.
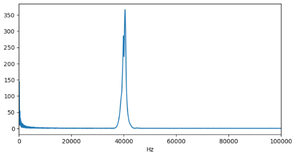
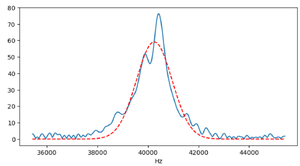
We perform a Fourier Transform on the received waveform to analyze its frequency content. The Fourier transform result is as follows:
From this plot, we observe that the received waveform contains a significant amount of low-frequency noise, which we need to filter out.
This low-frequency noise is common in laboratory environments and can originate from several sources:
- Power line interference: 50 Hz or 60 Hz noise from AC mains power is often present in lab equipment and cables.
- Electronic device vibrations: Fans, transformers, or other nearby equipment can produce low-frequency mechanical vibrations.
- Human activity and footsteps: Physical movement near the setup may introduce low-frequency noise through the table or sensor supports.
- Ambient acoustic noise: Conversations or nearby machinery can contribute sound energy at low frequencies.
To ensure accurate signal interpretation, especially in ultrasonic experiments, these noise components must be filtered out before further analysis.
Digital Filtering
To remove the background noise, we apply a digital filter. After filtering, the frequency spectrum and waveform are significantly improved, showing much less noise. We also fit the filtered frequency spectrum using a Gaussian (normal distribution) curve to estimate the dominant frequency component, which results in a mean frequency of 40012.77 Hz. The filtered results are shown below:
As shown, the noise is greatly reduced after filtering, making the waveform more suitable for experimental analysis.
Measurement of Sound Velocity
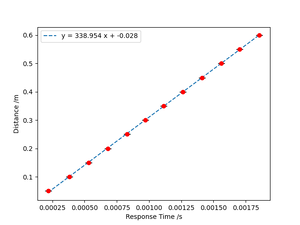
We measured waveforms from the detected sensor with various sensor-sensor distances. Considering the time difference between the transmitting sensor's waveform and the detecting sensor's waveform as the response time that the ultrasonic wave spreads this distance, we plotted the response time versus distance curve as follows:
In this plot, we can find the slope in the fitted curve around 338.95 m/s, which is close to the theoretical air sound velocity (343 m/s), with an error of around 1.18%.
It is worth noting that the speed of sound in air is affected by several environmental factors:
- Temperature: Sound velocity increases with temperature. For example, at 20 °C, the velocity is approximately 343 m/s, but at 0 °C it drops to about 331 m/s.
- Humidity: Higher humidity levels can increase the sound speed because water vapor is less dense than dry air.
- Air pressure and altitude: At constant temperature, changes in pressure have minimal effect, but at high altitudes where both pressure and temperature drop, sound speed decreases.
- Gas composition: Sound speed also depends on the medium's composition. For instance, sound travels faster in helium than in air.
These factors may contribute to slight deviations between the measured and theoretical values.
Doppler Effect Measurement of Sound Velocity
In this section, we explore another method to measure the speed of sound using the **Doppler effect**. We move the ultrasonic receiver at a constant speed of 10 cm/s and analyze the frequency shift due to the relative motion between the transmitter and receiver.
Raw Waveform Observation
The waveform collected during receiver motion is shown below:
As we can see, the raw waveform contains significant noise — even more than the previous static measurement. This is mainly due to mechanical vibrations and irregular contact with the metal rail on which the ultrasonic receiver was moving. Metal surfaces can introduce:
- **High-frequency jitter** from mechanical contact irregularities,
- **Low-frequency rumble** due to structural vibrations,
- **Reflections and scattering**, especially at non-uniform metal junctions.
Filtering and Signal Recovery
To isolate the useful frequency information, we apply digital filtering similar to the previous section. The filtered waveform and frequency spectrum are shown below:
The signal is now cleaner, and a clear frequency shift can be observed.
Doppler Effect Analysis
The Doppler effect equation for sound waves when the receiver is moving towards the stationary transmitter is:
\[ f' = f \left( 1 + \frac{v}{c} \right) \]
Where: - \( f' \) is the observed frequency, - \( f \) is the transmitted (original) frequency, - \( v \) is the velocity of the receiver (toward the source), - \( c \) is the speed of sound in air.
We rearrange the equation to solve for \( c \):
\[ c = \frac{v f}{f' - f} \]
We compute the measured sound velocity using the detected frequency shift. A comparison with the actual speed (10 cm/s) is shown below:
| Measured Frequency (Hz) | Original Frequency (Hz) | Velocity (cm/s) | Calculated Sound Speed (m/s) | Error (%) |
|---|---|---|---|---|
| ... | ... | 10 | ... | ... |
You can repeat this measurement at different speeds to further verify the consistency of the Doppler effect-based sound velocity estimation.