Ultrasonic Doppler Speedometer

Experiment

Ultrasonic Transmitter and Receiver

The core components of our experiment are the ultrasonic transmitter and ultrasonic receiver, which operate at a center frequency of approximately 40 kHz.

• The ultrasonic transmitter converts an electrical signal into mechanical vibrations to generate high-frequency sound waves that propagate through the air.
• The ultrasonic receiver does the reverse—it converts incoming ultrasonic waves into electrical signals for analysis.

These transducers rely on the piezoelectric effect, where certain materials produce voltage when subjected to mechanical stress (and vice versa). They are commonly used in range-finding, object detection, and motion sensing applications.

Oscilloscope

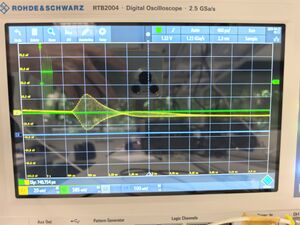
To visualize the waveforms generated and received, we use a digital oscilloscope. It allows us to observe and record time-domain signals in real-time, especially the transmitted pulse and its delayed echo after reflection or propagation.

Circuit Connections

The experimental circuit consists of three main components: the signal generator (or function output) from the oscilloscope, the ultrasonic transmitter, and the ultrasonic receiver. The connections are arranged as follows:

• The oscilloscope generates a square wave signal (~40 kHz), which is fed into the ultrasonic transmitter.
• The transmitter converts this signal into ultrasonic waves that propagate through the air.
• These waves are captured by the ultrasonic receiver, which converts them back into an electrical signal.
• Both the transmitted and received signals are connected to separate channels on the oscilloscope, enabling simultaneous real-time comparison.

This configuration allows for precise time-of-flight (ToF) measurement, necessary for calculating sound velocity and Doppler shifts.

Methods and Results

Measurement of Sound Velocity

In this section, we focus on measuring the velocity of sound using ultrasonic waves. By analyzing the time-of-flight (ToF) data between the transmitted and received signals, we estimate the distance and calculate the sound velocity. This approach uses experimental measurements from multiple sensor distances to create a response time versus distance curve, which is then analyzed to estimate the speed of sound in air.

Raw Data

First, we display the waveform shown on the oscilloscope. The following image shows the transmitted and received waveforms.（Take a distance of 10cm as an example）

Waveform Analysis and Fourier Transform

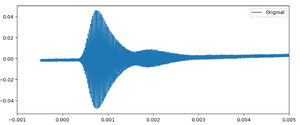
Next, we analyze the waveforms using Python. The transmitted waveform is a square wave, while the received waveform is more complex, resembling a sinusoidal waveform that is a sum of many sine waves.

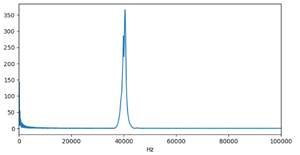
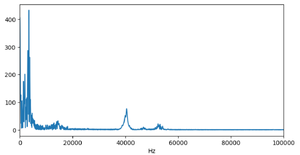
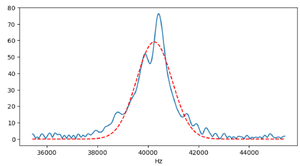
We perform a Fourier Transform on the received waveform to analyze its frequency content. The Fourier transform result is as follows:

From this plot, we observe that the received waveform contains a significant amount of low-frequency noise, which we need to filter out.

This low-frequency noise is common in laboratory environments and can originate from several sources:

• Power line interference: 50 Hz or 60 Hz noise from AC mains power is often present in lab equipment and cables.
• Electronic device vibrations: Fans, transformers, or other nearby equipment can produce low-frequency mechanical vibrations.
• Human activity and footsteps: Physical movement near the setup may introduce low-frequency noise through the table or sensor supports.
• Ambient acoustic noise: Conversations or nearby machinery can contribute sound energy at low frequencies.

To ensure accurate signal interpretation, especially in ultrasonic experiments, these noise components must be filtered out before further analysis.

Digital Filtering

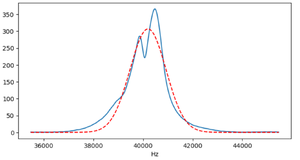
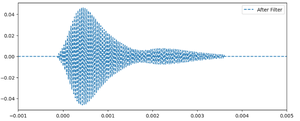
To remove the background noise, we apply a digital filter. After filtering, the frequency spectrum and waveform are significantly improved, showing much less noise. We also fit the filtered frequency spectrum using a Gaussian (normal distribution) curve to estimate the dominant frequency component, which results in a mean frequency of 40012.77 Hz. The filtered results are shown below:

As shown, the noise is greatly reduced after filtering, making the waveform more suitable for experimental analysis.

Reasults

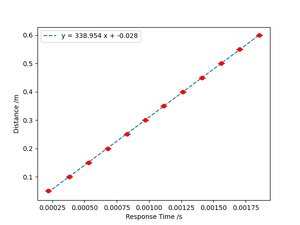
We measured waveforms from the detected sensor with various sensor-sensor distances. Considering the time difference between the transmitting sensor's waveform and the detecting sensor's waveform as the response time that the ultrasonic wave spreads this distance, we plotted the response time versus distance curve as follows:

In this plot, we can find the slope in the fitted curve around 338.95 m/s, which is close to the theoretical air sound velocity (343 m/s), with an error of around 1.18%.

It is worth noting that the speed of sound in air is affected by several environmental factors:

• Temperature: Sound velocity increases with temperature. For example, at 20 °C, the velocity is approximately 343 m/s, but at 0 °C it drops to about 331 m/s.
• Humidity: Higher humidity levels can increase the sound speed because water vapor is less dense than dry air.
• Air pressure and altitude: At constant temperature, changes in pressure have minimal effect, but at high altitudes where both pressure and temperature drop, sound speed decreases.
• Gas composition: Sound speed also depends on the medium's composition. For instance, sound travels faster in helium than in air.

These factors may contribute to slight deviations between the measured and theoretical values.

Doppler Effect Measurement of Sound Velocity

In this section, we explore another method to measure the speed of sound using the Doppler effect. We move the ultrasonic receiver at a constant speed of 10 cm/s and analyze the frequency shift due to the relative motion between the transmitter and receiver.

Raw Waveform Observation

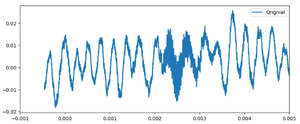
The waveform collected during receiver motion is shown below（Take a distance of 10cm/s as an example）:

As we can see, the raw waveform contains significant noise — even more than the previous static measurement.

This is mainly due to mechanical vibrations and irregular contact with the metal rail on which the ultrasonic receiver was moving. Metal surfaces can introduce:

• High-frequency jitter from mechanical contact irregularities,
• Low-frequency rumble due to structural vibrations,
• Reflections and scattering, especially at non-uniform metal junctions.

Filtering and Signal Recovery

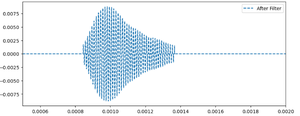
To isolate the useful frequency information, we apply digital filtering similar to the previous section. The filtered waveform and frequency spectrum are shown below:

The signal is now cleaner, and a clear frequency shift can be observed. Taking the case of a receiver moving at 10 cm/s as an example, the mean frequency after filtering is approximately 40245.66 Hz, which is noticeably higher than the stationary case (≈40012.77 Hz). This shift is consistent with the expected Doppler effect caused by motion toward the source.

Doppler Effect Analysis

The Doppler effect equation for sound waves when the receiver is moving towards the stationary transmitter is:

$f^{\prime }=f(1+\frac{v}{c})$

Where:

• $f^{\prime }$ is the observed frequency,
• $f$ is the transmitted (original) frequency,
• $v$ is the velocity of the receiver (toward the source),
• $c$ is the speed of sound in air.

We rearrange the equation to solve for $c$:

$c=\frac{vf}{f^{\prime }-f}$

We compute the measured sound velocity using the detected frequency shift. A comparison with the actual speed (10 cm/s) is shown below:

Measured Frequency (Hz)	Original Frequency (Hz)	Calculated Velocity (cm/s)	Actual Velocity (cm/s)	Error (%)
40019.85	40012.77	0.60	1	40.00
40072.61	40012.77	5.05	2	152.50
40115.24	40012.77	8.65	5	73.00
40245.66	40012.77	19.67	10	96.70
40745.79	40012.77	61.00	15	306.67

While the calculated velocities show significant errors, the magnitudes are correct. Possible reasons for the discrepancies include:

• Inaccurate Velocity Estimation: The velocity was estimated without precise measurement tools, leading to inconsistencies.
• Low Velocity Sensitivity: The Doppler effect is more accurate at higher velocities (typically > 1 m/s). At low speeds, the frequency shift is minimal, which reduces accuracy.
• Environmental Noise: Conducting the experiment on a metal rail may have introduced vibrations and noise that affected the results.
• Limited FFT Resolution: Small frequency shifts require high time resolution for accurate detection, which may not have been achieved here.
• Multipath Interference: Reflections from surrounding surfaces could distort the received signal.

Despite these issues, the results demonstrate the general applicability of the Doppler effect for velocity estimation.

Appendix

Python Code for Signal Processing and Sound Speed Estimation

 import pandas as pd
 import numpy as np
 import matplotlib.pyplot as plt

 def process_ultrasound_csv(file_path, encoding='utf-8', sound_speed=343):
     df = pd.read_csv(file_path, usecols=[0, 1, 2], encoding=encoding, skip_blank_lines=True)
     df.columns = ['时间', '接收信号', '输出信号']

     time = df['时间'].values
     tx = df['输出信号'].values
     rx = df['接收信号'].values

     tx_threshold = 0.5 * (np.max(tx) - np.min(tx)) + np.min(tx)
     tx_index = np.argmax(tx > tx_threshold)
     tx_time = time[tx_index]

     rx_index = np.argmax(rx)
     rx_time = time[rx_index]

     tof = rx_time - tx_time
     distance_estimated = tof * sound_speed

     return {
         'tx_time': tx_time,
         'rx_time': rx_time,
         'tof': tof,
         'distance_estimated': distance_estimated
     }
 def process_multiple_ultrasound_files(file_paths_dict, encoding='utf-8', sound_speed=343):
     results = {}
     for distance_cm, file_path in file_paths_dict.items():
         result = process_ultrasound_csv(file_path, encoding=encoding, sound_speed=sound_speed)
         results[distance_cm] = result
     return results

 def plot_estimated_vs_actual(results_dict):
     actual = []
     estimated = []
     for distance_cm, res in results_dict.items():
         actual.append(distance_cm / 100)
         estimated.append(res['distance_estimated'])

     coeffs = np.polyfit(actual, estimated, deg=1)
     fitted = np.polyval(coeffs, actual)

     plt.figure(figsize=(6, 6))
     plt.scatter(actual, estimated, color='dodgerblue', label='Estimated distance')
     plt.plot(actual, fitted, 'r-', label=f'fitting: y = {coeffs[0]:.3f}x + {coeffs[1]:.3f}')
     plt.xlabel('Actual distance (m)')
     plt.ylabel('Estimated distance (m)')
     plt.title('Actual distance vs Estimated distance')
     plt.legend()
     plt.grid(True)
     plt.axis('equal')
     plt.tight_layout()
     plt.show()

 file_paths = {
     cm: fr"C:\Users\70905\Downloads\WFM\WFM\WFM_{cm}cm_01.CSV"
     for cm in range(5, 65, 5)
 }

 all_results = process_multiple_ultrasound_files(file_paths)

 for distance_cm, res in all_results.items():
     print(f"{distance_cm}cm: ToF = {res['tof']:.6f}s, Estimated distance = {res['distance_estimated']:.3f}m")

 plot_estimated_vs_actual(all_results)

Python Code for Doppler Effect Signal Processing

 import numpy as np
 import math
 import matplotlib.pyplot as plt
 import pandas as pd
 from scipy.optimize import curve_fit
 from scipy.stats import norm

 file_dir = f'C:\\Users\\70905\\Documents\\WeChat Files\\wxid_msmjcahnii2f22\\FileStorage\\File\\2025-04\\WFM\\WFM\\WFM_10cm_01.CSV'
 df = pd.read_csv(file_dir)

 signal = df['C1 in V'].values
 T = df['in s'].values

 dt = T[2] - T[1]
 n = len(signal)
 N_pad = 50 * n
 signal_padded = np.zeros(N_pad)
 signal_padded[:n] = signal

 fft_vals = np.fft.fft(signal_padded)
 freqs = np.fft.fftfreq(N_pad, dt)

 pos_mask = freqs >= 0
 freqs = freqs[pos_mask]
 fft_vals = fft_vals[pos_mask]
 amplitudes = np.abs(fft_vals)
 max_index = np.argmax(amplitudes[5000:])
 dominant_freq = freqs[max_index + 5000]
 print(f"{dominant_freq} Hz")

 plt.figure(figsize=(8, 4))
 plt.plot(freqs, amplitudes)
 plt.xlim(0, 1e5)
 plt.xlabel('Hz')
 plt.show()

 def gauss(x, amp, mean, sigma):
     return amp * np.exp(-(x - mean) ** 2 / (2 * sigma ** 2))

 cutoff_freq = 5000
 filter_mask1 = np.abs(freqs) < dominant_freq + cutoff_freq
 filter_mask2 = np.abs(freqs) > dominant_freq - cutoff_freq
 filter_mask = filter_mask1 * filter_mask2
 filtered_fft = fft_vals * filter_mask
 filtered_fft2 = np.abs(filtered_fft.copy())
 idx_sorted = np.argsort(filtered_fft2)
 second_idx = idx_sorted[-1]

 freq_filtered = freqs[filter_mask]
 amplitudes_filtered = np.abs(filtered_fft[filter_mask])

 initial_guess = [np.max(amplitudes_filtered), dominant_freq, np.std(freq_filtered)]
 params, covariance = curve_fit(gauss, freq_filtered, amplitudes_filtered, p0=initial_guess)

 amp_fit, mean_fit, sigma_fit = params
 print(f"Fitted Gaussian parameters:")
 print(f"Amplitude: {amp_fit}")
 print(f"Center frequency: {mean_fit:.2f} Hz")
 print(f"Standard deviation: {sigma_fit:.2f} Hz")

 x_fit = np.linspace(np.min(freq_filtered), np.max(freq_filtered), 1000)
 y_fit = gauss(x_fit, *params)

 plt.figure(figsize=(8, 4))
 plt.plot(freq_filtered, amplitudes_filtered)
 plt.plot(x_fit, y_fit, label="Gaussian Fit", linestyle="--", color="red")
 plt.xlabel('Hz')
 plt.show()

 filtered_signal = np.fft.ifft(filtered_fft)
 filtered_signal = np.real(filtered_signal)[:n]

 plt.figure(figsize=(10, 4))
 plt.plot(T, signal, label='Original')
 plt.xlim(-0.001, 0.005)
 plt.legend()
 plt.show()

 T2 = np.linspace(T[0], T[-1], len(filtered_signal))
 B = []
 s = 15e-4
 Tr = 0
 for i in range(len(T2)):
     if abs(filtered_signal[i]) >= s:
         B.append(1)
         if Tr == 0:
             Tr += 1
     else:
         B.append(0)
 filtered_signal = filtered_signal * np.array(B)

 plt.figure(figsize=(10, 4))
 plt.plot(T2 * math.pi, filtered_signal, label='After Filter', linestyle='--')
 plt.xlim(-0.001, 0.005)
 plt.legend()
 plt.show()