Laser Distance Measurer

Group Members

Arya Chowdhury, Liu Sijin, Jonathan Wong

Background and Theory

Laser-based distance measurement is a technique to measure distances remotely when on-site measurement becomes inconvenient. This has many applications such as autonomous driving, radar, and precision manufacturing. The working principle of using lasers to measure such distances can generally be categorised into one of three approaches: pulsed time-of-flight (ToF), optical triangulation and phase-shift continuous-wave (CW) measurement[1]. Here we will construct an apparatus according to the third approach.

Mathematical Background on Phase-Shift Distance Measurement

When a CW laser is intensity-modulated at frequency $f_m$, round-trip propagation to a target introduces a phase delay

$\mathrm{\Delta }\varphi =\frac{4\pi d}{{\lambda }_m},{\lambda }_m=\frac{c}{f_m}$,

where d is the one-way distance and c is the speed of light[2]. Solving for d gives

$d=\frac{{\lambda }_m\mathrm{\Delta }\varphi }{4\pi }=\frac{c\mathrm{\Delta }\varphi }{4\pi f_m}.$

Because phase is measured modulo $2\pi$, the maximum unambiguous range is

$d_{\text{max}}=\frac{c}{2f_m}.$[3]

For $f_m=10\text{MHz}$, $d_{\text{max}}\approx 15\text{m}$, adequate for laboratory-scale demonstrations.

Note: Advantages of Phase-delay measurement

The phase-shift measurement method is preferred over pulsed ToF and optical triangulation whenever sub-millimetre accuracy, compact hardware and real-time operation are simultaneously required[4]. Because the technique extracts distance from the phase of a continuous, MHz-rate modulation rather than from absolute travel time or geometric baselines, it can achieve high precision with modest electronic bandwidths and without bulky optical assemblies. The use of continuous-wave illumination allows the transmitter to run at low peak power, simplifying driver circuitry and easing eye-safety constraints, while the reliance on differential phase makes the measurement intrinsically insensitive to slow amplitude drifts, laser-power fluctuations or partial signal obscuration. These attributes enable lightweight, low-cost sensor heads that are well suited to embedded or mobile platforms[5], and they motivate a bottom-up investigation of how modulation linearity, detector bandwidth and amplifier noise ultimately set the achievable accuracy ceiling[6].

Equipment List

1. Oscilloscope
2. Function generator that can output square wave signal (model used: Tektronix AFG1022)
3. DC power supply for photodetector (model used: Keithley 2231A-30-3)
4. Hamamatsu S5971 silicon photodetector
5. 650 nm (red) LED
6. Collimating lens to mount on the LED
7. Mirror
8. Translation stage
9. Optical breadboard, postholders and screws
10. Ruler or measuring tape
11. BNC cables

Experimental Work

Laser Modulation and System Initialisation

Configure the function generator to output a 10 MHz square wave with an amplitude of 0–3.1 V (High level: 3.1 V, Low level: 1.0 V, output impedance: 50 Ω) to modulate the laser diode. Use the DC power supply to provide 5.0 V to the laser driver circuit, with a current limit of 30 mA. Verify the laser beam stability to avoid multimode noise or thermal drift that could distort the modulation waveform.

Optical Alignment

Mount the 650 nm laser diode and use an aspheric lens to collimate and focus the beam onto the reflective target surface.

Figure 1. Front view of collimating lens for laser diode	Figure 2. Side view of collimating lens for laser diode

Detection and Amplification Circuit Configuration

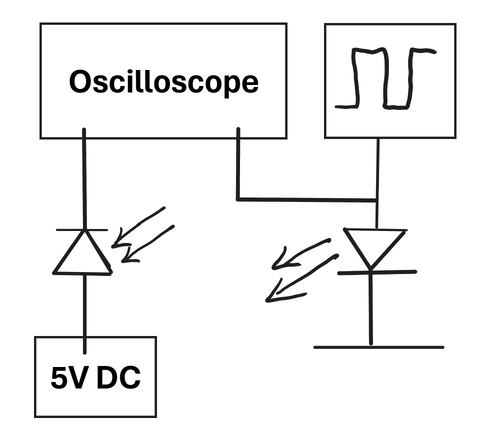
For the photodetector, use the Hamamatsu S5971 silicon photodiode to detect the reflected light signal. To amplify the signal linearly without saturation, connect the detector output to a matched high-speed preamplifier (bandwidth >100 MHz, gain ∼10³–10⁵). Connect the amplifier output to Channel 2 of a digital oscilloscope; connect the reference signal from the function generator to Channel 1 as the modulation phase reference.

Figure 3. Hamamatsu S5971 silicon photodiode with amplifier

Time Delay vs. Distance Mapping

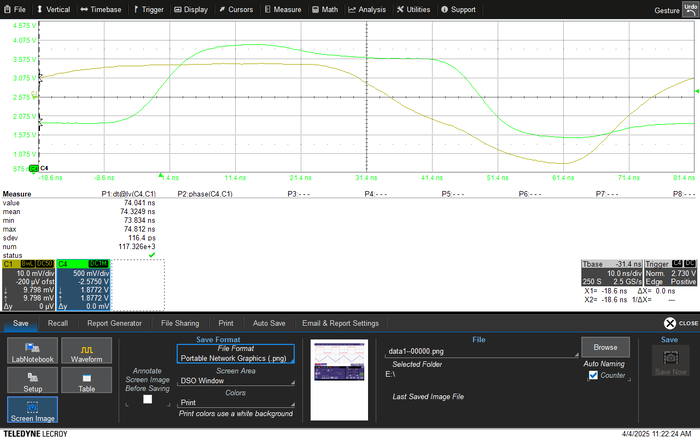
Fix the LED source and the photodetector on a linear translation stage, ensuring proper alignment for the beam return to the detector at all positions along the translation stage; the detector and the laser diode were mounted on a postholder so that the height of the detectors was adjustable. Turn on the LED and ensure that the beam is collimated by adjusting the distance of the lens to the LED. Incident the LED onto the photodetector and observe the function generated on the oscilloscope. Use the oscilloscope’s cursor measurement function to determine the relative time delay Δt between the modulation reference signal (Channel 1) and the return signal (Channel 2). Correlate the measured delay values with corresponding distances to establish the system’s delay–distance response curve. The following are the steps carried out to measure the time delay and the corresponding distance:

1. Fix the LED source and the photodetector on a linear translation stage, ensuring proper alignment for the beam return to the detector at all positions along the translation stage; the detector and the laser diode were mounted on a postholder so that the height of the detectors was adjustable.
2. Use a meter ruler to mark the distance along the translation stage.
3. Move the LED source to the marked positions (e.g. 30 cm from detector) and adjust the beam until it is centralised on the photodetector.
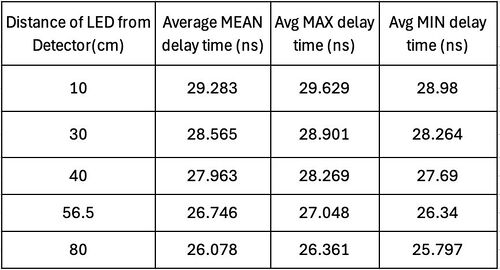
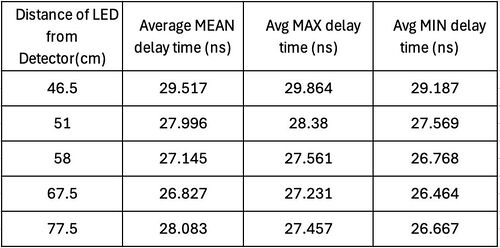
4. Measure the time delay on the oscilloscope. Record the minimum, maximum and mean time delay—take three readings per distance and average them.
5. Repeat steps 1–4 for different distances on the translation stage.
6. Insert a mirror in the setup to act as the “object we are trying to measure the distance of”, so that the beam path is reflected off the mirror to the photodetector.
7. Measure the total path length manually and repeat steps 1–4 for each mirror position.

Schematic of experiment setup (without mirror). If the photodiode is in line with and can receive light from the LED, two waveforms (one from the source LED and one from the photodiode) will be shown on the oscilloscope.

Figure 4. Measurement experimental setup without mirror: LED and photodetector on translation stage.

Figure 5. Measurement experimental setup with mirror acting as the “object.”

Results

Figure 6. Delay between the function generator and the received signal by the photodetector on the oscilloscope. Green graph represents the function generated by the function generator and the yellow graph represents the function produced from received the laser beam by the detector.

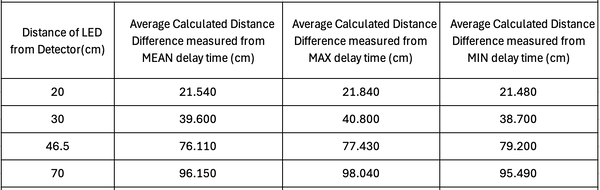
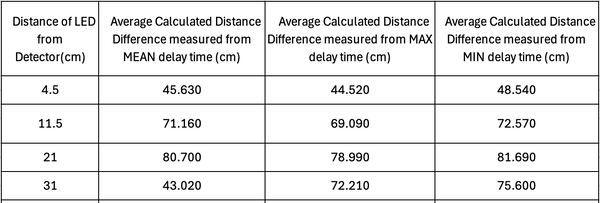
Table 1. Measured delay time vs manually measured distance between LED and photodetector	Table 2. Measured delay time vs manually measured distance with mirror acting as the “object.”

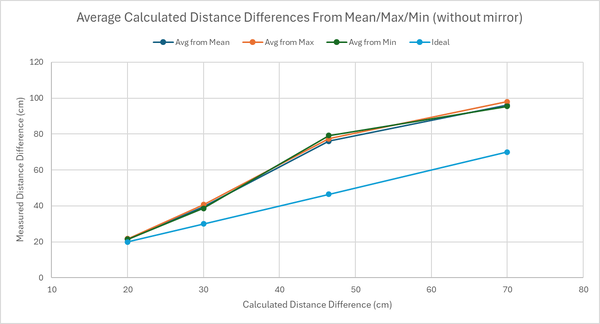
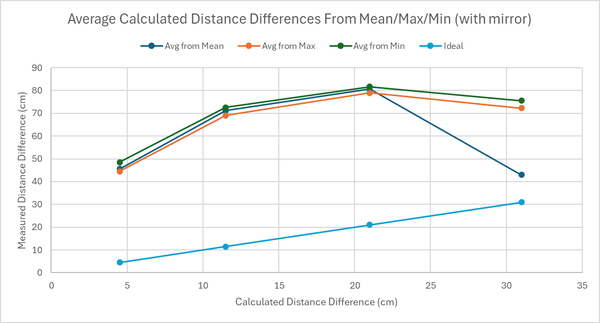
The measured delay time is in the order of 20-30 nanoseconds, which, when calculated, gives about 6-9m of distance. However, our incremental changes in the distance between the LED and the photodetector were in the order of 10-80cm. Hence, it was evident that this additional delay time was occurring due to all the cables attached to the oscilloscope and function generation and the distance between the laser and the detector. To account for this, we took the shortest distance as our reference distance. The difference between the successive measured distances and the shortest distance gives us the "absolute" distance. We can refer to this as distance difference. We can do this for the measured delay time as well. Take the delay time for the shortest manually measured distance and subtract it from the successive delay times to get an absolute delay time. Another method we thought of was simply plotting a linear plot of manually measured distance vs the delay time and obtaining the y-intercept, which would be the additional delay time due to the system and the cables. One could then subtract this additional delay time from the system from each measured delay time. However, when we measured the gradient of this linear plot on multiple days, the gradient was slightly different each time the measurements were carried out. Hence, we decided to adopt the former approach.

Table 3. Calculated Average Distance Difference from delay time vs Manually measured distance between LED and photodetector. Separation distance of 10cm was taken as the "reference" distance and the successive distances were subtracted from it to give "absolute" values.	Table 4. Calculated Average Distance Difference from delay time vs Manually measured distance between LED and photodetector with the mirror acting as the "object". Separation distance of 46.5cmwas taken as the "reference" distance and the successive distances were subtracted from it to give "absolute" values.

Figure 7. Graph of Calculated Average Distance Difference from delay time vs manually measured distance difference between LED and photodetector without mirror.	Figure 8. Graph of Calculated Average Distance Difference from delay time vs manually measured distance difference between LED and photodetector with a mirror acting as the "object"

Challenges and Conclusion

1. One of the challenges we faced was centring the beam onto the photodetector. Due to the lack of a focusing beam on the photodetector, the laser beam spot size was much larger than the surface area of the photodetector. What this led to was a constant fluctuation of the delay time on the oscilloscope as the brightest part of the beam was not always centred on the photodetector despite optimising stabilisation of the beam path.
2. To have accurate distance measurements in the centimetre regime, the delay time we required was ~0.3ns for every 10cm. However, the fluctuation of the delay time on the oscilloscope was causing the 1st decimal place to fluctuate constantly.

Figure 9. Beam spot on photodetector

Though the project's concept was fairly straightforward, the yielded results were not precise within the instruments' uncertainty. This points to experimental errors, such as the lack of a focusing mirror, which caused fluctuations in the delay. The data obtained from calculating the distance difference is ~20-30cm higher than the manually measured distance, which makes it quite inaccurate. To reduce the inaccuracies, the measured distance difference can be larger, in the order of meters. This would mean that the changes in the delay would be in the order of a few nanoseconds rather than a few tenths of a nanosecond, reducing the error from the fluctuation. However, aligning the LED onto the detector would be even more difficult and might cause more fluctuations on the delay if there is no focusing lens.

Improvements and Future Work

1. Install a focusing lens for the photodetector to reduce the fluctuation of the time delay on the oscilloscope.
2. Use a bandpass filter at 650 nm laser to filter out other frequencies to get less fluctuations in the delay time reading on the oscilloscope.
3. Longer translating stage for longer distance measurement

References

[1] Blais, F. (2004). Review of 20 Years of Range Sensor Development. Journal of Laser Applications, 17(4), 208–220. [1]

[2] Wu, D. (2022). Phase-Shift Laser Ranging Technology Based on Multi-Frequency Modulation. Photonics, 9(9), 603. [2]

[3] Li, Y. (2023). Phase-Modulated Continuous-Wave Coherent Ranging Method for High-Precision Measurement. Optics Express, 31(4), 6514–6524. [3]

[4] Park, J. (2018). Multi-tone Modulated Continuous-Wave LiDAR, Proceedings of SPIE. [4]

[5] Liu, M. (2024). Deep Neural Network-Based Phase-Modulated Continuous-Wave LiDAR. Sensors, 24(5), 1617. [5]

[6] Ho, T. (1998). Error Analysis of Phase-Shift Laser Rangefinder with High-Level Signal. Sensors and Actuators A, 66(1–3), 110–115. [6]