Inductor Sensors of Ultra-high Sensitivity Based on Nonlinear Exceptional Point

Introduction

We are building two coupled oscillating circuits: one that naturally loses energy (lossy) and one that gains energy (active) using a specific amplifier that saturates at high amplitudes. When tuning these two circuits to a nonlinear Exceptional Point (NEP), the system becomes extremely sensitive to small perturbations in inductance, following a steep cubic-root response curve, while remaining resistant to noise.

Team Members

Wang Peikun E1538091@u.nus.edu

Zhu Ziyang E1583446@u.nus.edu

Yuan Si-Yu siyu_yuan@u.nus.edu

Li Xunyu xunyu@u.nus.edu

Setups

Experimental setups

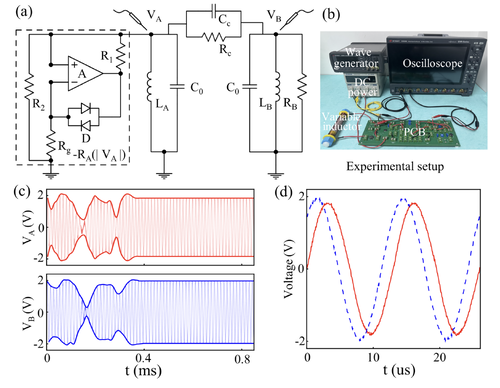
In FIG. 1 adopted from Ref. 1, we present:

(a) Schematic of the circuit comprising inductors ($L$), capacitors ($C$), resistors ($R$), diodes ($D$), and an amplifier ($A$). The dashed rectangle indicates the negative resistance element, $-R_A(|V_A|)$.

(b) Photograph of the experimental setup. An oscilloscope records the waveforms of $V_A$ and $V_B$ to derive frequency, voltage, and relative phase data. A DC unit powers the amplifier, while an arbitrary waveform generator provides the external driving signal. A variable inductor allows for fine-tuning of $L_A$ to control the resonance frequency of resonator $A$.

(c) Temporal dynamics of $V_A$ (red) and $V_B$ (blue) following the cessation of a 1 V, 70 kHz external driving signal. The system achieves a stable state at approximately 0.4 ms. Bold lines depict the signal envelopes, which remain constant after stabilization.

(d) Magnified view of the stable state dynamics beginning at 0.66 ms. Experimental parameters are: $L_A=245.4\mu \mathrm{H}$, $C_0=18.5\mathrm{n}\mathrm{F}$, $C_c=3.9\mathrm{n}\mathrm{F}$, $R_c=760\mathrm{\Omega }$, $R_B=1314\mathrm{\Omega }$, and $L_B=197.7\mu \mathrm{H}$.

Measurements

...

Results and Analysis

...

References

[1] K. Bai, T.-R. Liu, L. Fang, J.-Z. Li, C. Lin, D. Wan, and M. Xiao, Observation of nonlinear exceptional points with a complete basis in dynamics, Phys. Rev. Lett. 132, 073802 (2024).