Magnetic field sensing using a fluxgate magnetometer

Introduction to magnetic field sensing

Magnetic field sensing plays a crucial role in both scientific research and practical applications, ranging from searching for fundamental physics, geophysical nagigations, to industrial and biomedical uses. Magnetic sensors are used to detect, map, and measure the intensity and direction of magnetic fields. There are several methods for sensing magnetic fields, and the choice of sensor depends on the application requirements, such as sensitivity, bandwidth, and environmental robustness.

Different types of magnetometers

• Fluxgate magnetometers use ferromagnetic cores and detect magnetic fields by sensing nonlinear changes in core permeability. They are valued for their robustness and precision in low-field measurements, making them ideal for space missions and geological studies.

• SQUID magnetometers (Superconducting Quantum Interference Devices) are among the most sensitive magnetic field detectors. Operating at cryogenic temperatures, SQUIDs exploit quantum interference in superconducting loops to detect fields as small as femtoteslas. They are widely used in biomagnetism (e.g., MEG – magnetoencephalography) and in fundamental physics experiments.

• Optically pumped magnetometers rely on the interaction between light and spin-polarized atoms, typically alkali metals like rubidium or cesium. These sensors can achieve extreme sensitivity while operating at room temperature <ref>Template:Cite journal</ref>. The most sensitive optical magnetometers, such as spin-exchange relaxation-free (SERF) devices, can reach sensitivities below 1 fT/√Hz, rivaling superconducting magnetometers. More compact or portable designs, while less sensitive, still operate effectively in the picotesla to nanotesla range, making them attractive for biomedical, navigation, and remote sensing applications.

• Hall effect sensors are solid-state devices that measure the voltage generated by a magnetic field perpendicular to an electric current. They are simple, low-cost, and widely used in consumer electronics and industrial systems where high sensitivity is not critical.

• Magnetoresistive sensors (AMR, GMR, TMR) rely on changes in resistance due to the presence of a magnetic field. They offer high bandwidth and miniaturization potential, useful in automotive and robotics applications.

• Proton precession and Overhauser magnetometers use nuclear magnetic resonance techniques to measure absolute magnetic field strength with high accuracy, commonly applied in geophysical surveys.

Each of these technologies offers a unique combination of sensitivity, size, cost, and operational constraints.

Applications

Magnetic sensors find applications across a wide spectrum of fields:

• In fundamental physics, they are used in searches for exotic particles and precision measurements of fundamental constants.
• In geophysics, magnetometers are employed for mineral exploration, archaeology, and mapping Earth's magnetic field.
• In navigation, especially in aerospace and underwater contexts, magnetic sensing provides orientation and heading information where GPS is unavailable.
• In the biomedical field, ultra-sensitive magnetometers (e.g., SQUID and optical) enable non-invasive detection of weak magnetic signals from the brain and heart.
• In industry, they are used for non-destructive testing, monitoring electric motors, and detecting ferrous materials in quality control.

Modern advances in materials science, quantum optics, and electronics continue to expand the reach and capability of magnetic field sensing technologies.

Operation principles of a fluxgate magnetometer

How does a fluxgate magnetometer work?

A fluxgate magnetometer works by exploiting the magnetic response of a ferromagnetic core to detect an external magnetic field. It detects changes in magnetic permeability $\mu$ due to the presence of an external field, typically producing a signal at 2nd harmonic of the excitation frequency. In a fluxgate sensor, the core material has very high magnetic permeability, meaning the core material can concentrate magnetic fields very well. Besides, it reacts strongly to changes in external fields. Its permeability changes nonlinearly as the material saturates, which is crucial for generating detectable signals (like the 2nd harmonic) when there's an external field.

Specifically, as shown in Figure 1, the core of a typical fluxgate magnetometer consists of two identical ferromagnetic rods with magnetic permeability $\mu$, each wrapped with a coil through which an alternating driving current flows in opposite directions. This setup generates magnetic fields $B_1=\mu H_1$ and $B_2=\mu H_2$ that are also in opposite directions, where $H_1$ and $H_2$ are auxiliary magnetic field generated by the coils. These coils are driven by a time-varying current (Figure 1b), typically a square wave. A secondary (sensing) coil is placed around both of the two cores to detect changes in net magnetic flux. In the absence of an external magnetic field, the opposing magnetizations $B_1$ and $B_2$ cancel out exactly, resulting in zero net magnetic flux through the sensing coil. Therefore, no voltage is induced in the sensing coil.

Figure 1: (a) Illustration of a fluxgate with two parallel ferromagnetic coils, (b) Illustration of an alternating driving wave and (c) the corresponding magnetic responses of the two ferromagnetic magnetic cores in the absence of external magnetic field

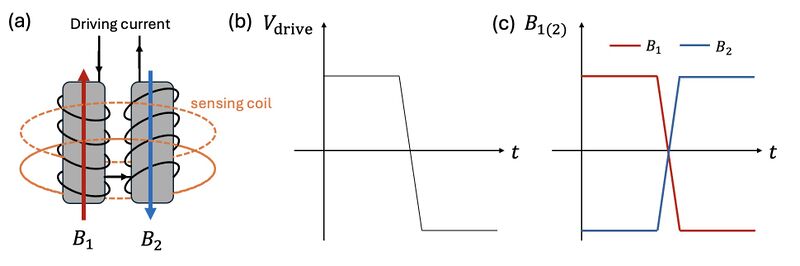
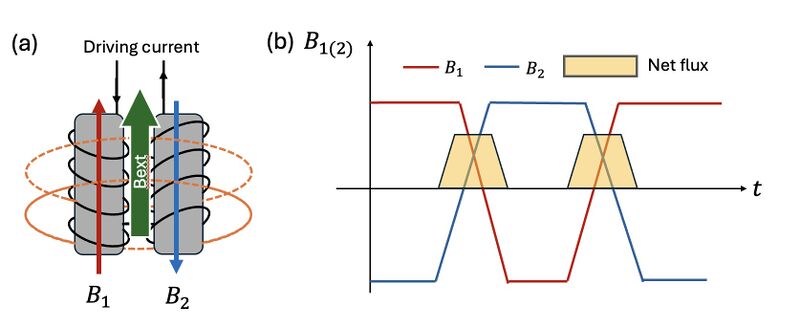
However, when an external magnetic field $B_{\text{ext}}$ is applied along the axis of the cores, it breaks the symmetry between the two magnetic responses (Figure 2b). This results in the emergence of non-zero total magnetic flux through the sensing coil. According to Faraday’s Law of Induction and Lenz’s Law, a time-varying magnetic flux $\mathrm{\Phi }(t)$ through the coil induces an electromotive force (EMF) $V_{\text{ind}}=-\frac{d\mathrm{\Phi }}{dt}$. As Figure 2b shows, the net flux induced voltage typically appears at twice the driving frequency and forms the output signal of the magnetometer, allowing detection of the external magnetic field.

Figure 2: (a) Illustration of a fluxgate in an external magnetic field, and (b) the corresponding magnetic responses of the two ferromagnetic magnetic cores, generating non-zero net magnetic flux in the sensing coil.

Manual of the 'Magnetic Field Sensor FLC 100' used in the experiment

The FLC 100 magnetic field sensor was used in this experiment. The magnetic sensor has a compact design, high sensitivity, and low noise characteristics, making it well-suited for measuring weak magnetic fields in a laboratory setting. The working parameters of the sensor are listed below:

Working parameters of the FLC 100 magnetic field sensor

Parameter	Value
Measurement range	±100 µT
Output voltage	±1 V per 50 µT (max ±2.5 V)
Reference output	2.5 V with respect to ground (OUT−)
Output impedance	<1 Ω
Load conditions	>1 kΩ resistance, <100 pF capacitance
Bandwidth	DC to 1 kHz (−3 dB)
Noise	<0.5 nT RMS (0.1–10 Hz), ~150 pT/√Hz at 1 Hz
Zero drift	<2 nT/K
Supply voltage	5 V ±5%
Supply current	~2 mA
Operating temperature	−40 °C to +85 °C
Dimensions	44.5 mm × 14 mm × 5.5 mm
Detection coil length	22 mm

Source: Stefan Mayer Instruments – FLC 100 Datasheet

Experiment

Setup of the experiment

In this experiment, a power supply provides a 5 V driving voltage for the fluxgate magnetometer (FLC100). The output signal from the magnetometer is monitored using an oscilloscope. A schematic of the experimental setup is shown below.

Figure 3: Schematic of the experiment setup

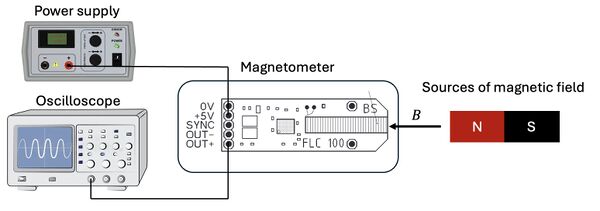
To demonstrate the basic operation of the magnetometer, a permanent magnet is used as a test source. As the magnet is moved in proximity to the sensor, changes in the output voltage are clearly observed, indicating a varying magnetic field, as the video below shows:

Click to download or view the magnetometer demonstration video.

For calibration purposes, in the following experiments, both a permanent magnet and a current-carrying coil are used. These sources allow characterization of the magnetometer's response under controlled magnetic field conditions.

Modeling and measurement of a permanent magnet

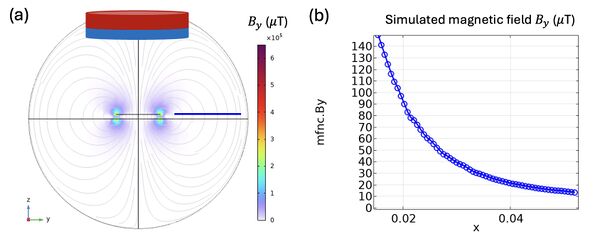
Firstly, a disk-shaped permanent magnet is used as the source of the magnetic field. The magnetic field distribution around the magnet is simulated using COMSOL Multiphysics, modeling the magnet as a disk with a diameter of 1.6 cm and a thickness of 3 mm. A stream plot of the three magnetic field components is shown in Figure 4(a). It is important to note that the magnetometer measures only the scalar component of the magnetic field, in our case, the $B_y$ is projected along the axis of the magnetometer. The component $B_y$ is evaluated along the blue cutline indicated in Figure 4(a), where it is observed to be very small—on the order of microtesla—because the magnetic field is predominantly out-of-plane near the disk.

Figure 4: (a) Simulation of magnetic field around a disk magnet (b) $B_y$ along the blue cut line in (a)

To experimentally validate the simulation results, we position the magnet adjacent to a fluxgate magnetometer and measure the magnetic field strength as a function of distance (Figure 5a). The measurements are repeated three times to ensure reproducibility. The measured voltages and the corresponding calculated magnetic field strengths are presented in Figures 5b and 5c, respectively.

Figure 5: (a) Schematic of measurement setup (b) Measured voltage when varying the distance between the disk magnet and the magnetometer, and (a) measured in-plane magnetic field $B_y$

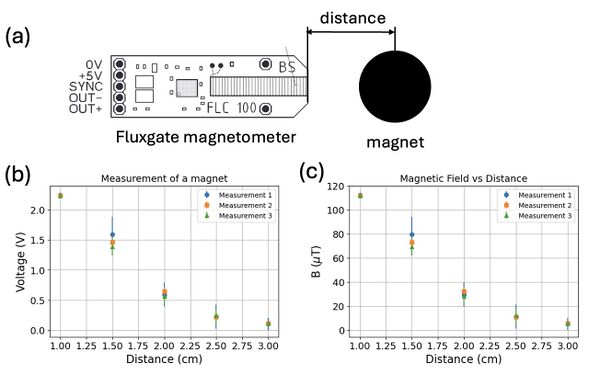
As expected, the magnetic field strength decreases with increasing distance from the magnet, following an approximate inverse relationship. The repeated measurements exhibit small variations, indicating good measurement consistency and reliability of the setup. Discrepancies between the experimental data and the simulation may be attributed to factors such as misalignments in positioning, imperfections in the magnet’s shape or magnetization, and environmental magnetic noise.

Modeling and measurement of a current carrying coil

In this section, we present the modeling and experimental measurement of the magnetic field generated by a current-carrying coil.

The coil used in the experiment is a toroidal solenoid, as illustrated in Figure 6. A toroidal solenoid consists of a wire wound in a circular shape, forming a doughnut-like structure. The inner radius of the toroid is around $a=0.3$cm, the outer radius is around 0.7cm, and the total winding number is 50.

One important characteristic of a toroidal solenoid is that its magnetic field is largely confined within the core of the toroid, with negligible field outside in ideal conditions. The magnetic field inside the toroid is expected to be strong and azimuthally symmetric, while the external field is significantly weaker.

To understand the behavior of the magnetic field, we performed numerical simulations to calculate the magnetic field distribution both inside and outside the toroid. The magnetic field inside the toroid is theoretically given by: $B(r)=\frac{{\mu }_{0}nI}{2\pi r}$

The simulation results reveal the expected strong field inside the toroid and a rapidly decaying, much weaker field outside.

Experimentally, we measured the magnetic field using a magnetometer. Due to the finite size and sensitivity range of the magnetometer probe, we were only able to reliably measure the magnetic field outside the toroid. Measuring inside the toroid would require a significantly smaller probe to fit within the core without disturbing the field distribution.

References

<references />